Cercle de Ford - Définition
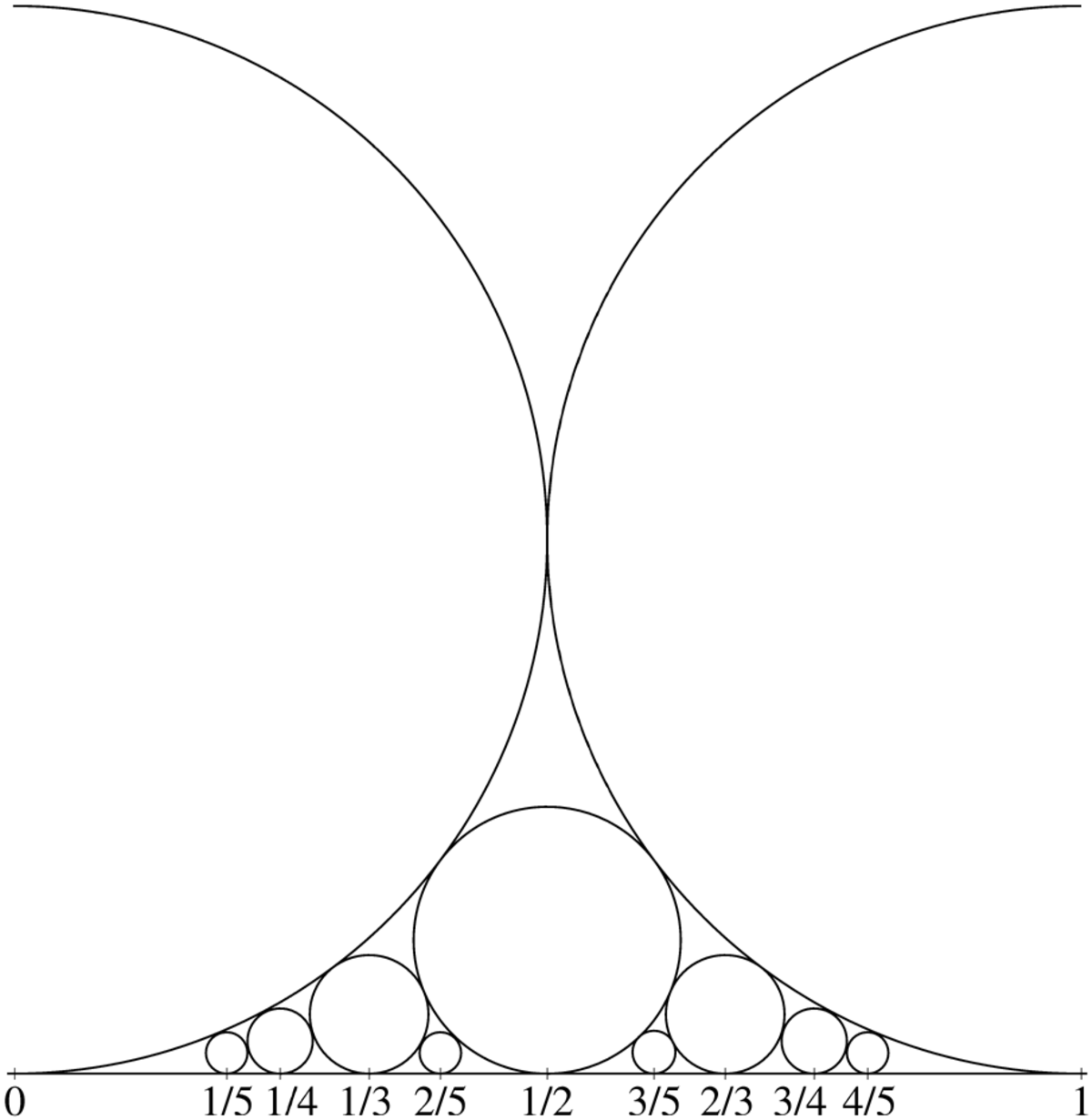
En mathématiques, le cercle de Ford est le cercle de centre (p/q, 1/2q2) et de rayon 1/(2q2) associé à la fraction irréductible p/q, une fractions composée des termes entiers les plus petits premiers entre eux.
Histoire
Les cercles de Ford sont nommés ainsi en l'honneur du mathématicien américain Lester Ford (père), qui les a décrits dans un article publié dans American Mathematical Monthly en 1938.
Propriétés
Le cercle de Ford associé à la fraction irréductibe p/q est noté C[p/q] ou C[p, q]. Par extension, la droite d'équation y = 1 est considérée comme un cercle de Ford — elle peut être assimilée à un cercle de Ford associé à l'infini, avec dans ce cas, p = 1, q = 0.
Deux cercles de Ford associés à deux fractions distinctes sont soit disjoints ou tangents. D'autre part, tout cercle de Ford est tangent à l'axe des abscisses. Si la fraction irréductible p/q est comprise entre 0 et 1, les cercles de Ford qui sont tangents à C[p/q] sont précisément ceux associés aux fractions qui sont les voisines de p/q dans certaines suites de Farey.
Les cercles de Ford peuvent aussi être assimilés à des courbes dans le plan complexe. Le groupe modulaire des transformations du plan complexe transforme les cercles de Ford en d'autres cercles de Ford.
En interprétant la moitié supérieure du plan complexe comme un modèle du plan hyperbolique (le modèle du demi-plan de Poincaré), les cercles de Ford peuvent aussi être interprétés comme un pavage du plan hyperbolique. Deux cercles de Ford quelconques sont congrus en géométrie hyperbolique. Si C[p/q] et C[r/s] sont des cercles de Ford tangents, alors le demi-cercle joignant (p/q, 0) et (r/s, 0) qui est perpendiculaire à l'axe des abscisses est une droite hyperbolique qui passe aussi par le point où les deux cercles sont tangents à un autre.
Les cercles de Ford forment un sous-ensemble des cercles d'Apollonius généré par les droites y = 0 et y = 1 et le cercle C[0/1].