Fraction continue - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
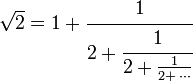
|
En mathématiques, une fraction continue ou fraction continue simple ou encore fraction continuée est une expression de la forme :
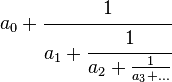
comportant un nombre fini ou infini d'étages. Une fraction continue généralisée est l'analogue d'une fraction continue, mais avec les 1 remplacés par des valeurs bj :
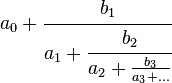
Le présent article porte principalement sur les fractions continues simples.
On montre qu'on peut représenter tout nombre réel sous forme d'une fraction continue, finie ou infinie, dans laquelle a0 est un entier relatif et les aj sont des entiers strictement positifs. Le sens du mot représenter sera précisé ultérieurement.
Comme dans la notation décimale usuelle, où chaque nombre réel est approché par des nombres décimaux de plus en plus précisément au fur et à mesure de la donnée des décimales successives, de même chaque nombre réel est approché par des fractions étagées de la forme ci-dessus de plus en plus précisément au fur et à mesure qu'on rajoute des étages. En outre, s'il faut une infinité de décimales pour décrire exactement un nombre non décimal, il faut un développement infini en fraction continue pour décrire exactement un nombre irrationnel.
Les fractions continues sont utiles en approximation diophantienne, notamment parce qu'elles fournissent, en un certain sens, les « meilleures » approximations des nombres réels par des nombres rationnels. Cette propriété est à l’origine d’algorithmes pour l’approximation de racines carrées, mais aussi de démonstrations d’irrationalité voire de transcendance pour certains nombres comme π ou e. La périodicité des fractions continues des racines carrées d’entiers strictement supérieurs à un et sans facteur carré a des conséquences utiles pour l’étude de l’équation de Pell-Fermat.
Déjà usitées chez les mathématiciens indiens au Moyen Âge, les fractions continues sont étudiées en Europe dès le XVIIe siècle et constituent encore un vaste sujet de recherche, près de 3 000 articles ont été publiés sur ce sujet au XXe siècle. Elles sont maintenant généralisées à d'autres expressions, appliquées à l'approximation de séries entières appelées approximant de Padé ou encore adaptées aux applications linéaires.

Tour d'horizon

La notion de fraction continue est vaste et se retrouve dans de nombreuses branches des mathématiques. Les concepts associés peuvent aussi bien être relativement simples comme l'algorithme d'Euclide ou beaucoup plus subtils comme une fonction méromorphe.
Il est possible, dans un premier temps, de voir une fraction continue comme une suite de nombres entiers qui représente un nombre réel. Cette situation est un peu la même que celle du système décimal qui représente π par la suite d'entiers 3, 1, 4, 1, 5, 9 ... Sous forme de fraction continue, la suite est 3, 7, 15, 292, 1, 1, ... Un premier champ d'étude consiste à étudier la relation entre la suite 3, 7, 15, 292, 1, 1, .... et celle des nombres rationnels que propose la fraction continue, en l'occurrence 3, 22/7, 333/106 etc, il permet de savoir comment passer de la première suite à la deuxième, comment la deuxième converge et répond à d'autres questions de cette nature. Tel est essentiellement l'objet de cet article.
Les fractions continues ont une relation particulière avec les racines carrées ou plus généralement les nombres, dits quadratiques, de la forme a + b.√d ou a et b sont des nombres rationnels et d un entier sans facteur carré. Les fractions continues associées sont périodiques, à partir d'un certain rang, c'est-à-dire que la suite des entiers formant la fraction continue se répète à partir d'un certain rang et jusqu'à l'infini. Cette situation est à l'image des représentations décimales infinies de nombres rationnels. Ces fractions continues permettent de résoudre un célèbre problème d'arithmétique appelé équation de Pell-Fermat. Cette question fait l'objet de l'article Fraction continue d'un nombre quadratique.
À l'image du système décimal, la fraction continue offre des nombres rationnels de plus en plus approchés de leur cible. Ces approximations sont bien meilleures que celles décimales. La deuxième approximation décimale de π, égale à 31/10 possède un dénominateur relativement proche de celui de la deuxième approximation de la fraction continue 22/7, en revanche 22/7 est plus de 30 fois plus précis que 31/10. Ce type d'approche d'un nombre réel par un nombre rationnel est appelé approximation diophantienne. Les fractions continues y jouent un grand rôle. Elles ont permis de construire le premier nombre transcendant connu ou de montrer que e la base du logarithme népérien est irrationnel. À condition de généraliser la définition d'une fraction continue, il devient possible de montrer que π est aussi irrationnel puis que ces deux derniers nombres sont transcendants. Cette approche est traitée dans l'article Fraction continue et approximation diophantienne.
Une fraction continue ne concerne pas uniquement les nombres mais aussi les fonctions. On construit des fractions continues généralisées en remplaçant les coefficients an et bn par des polynômes. Une motivation provient de l'analyse complexe, qui a pour objet l'étude des fonctions de la variable complexe à valeur complexe, ayant une bonne propriété de régularité appelée dérivabilité. L'approche classique consiste à construire une suite de polynômes de degré de plus en plus élevé, appelée série entière, et qui converge vers la fonction cible. Une spécificité fréquente, pour ce type de fonction est de posséder des pôles, c'est-à-dire des espèces de montagnes qui grimpent jusqu'à l'infini. Sa série entière ne permet pas de voir plus loin qu'un pôle. Si, au lieu d'approcher la fonction par des polynômes, on utilise des quotients, on construit des fractions continues appelées approximants de Padé. Elles possèdent le mérite de permettre de voir l'autre versant des pôles.
D'autres propriétés ont été étudiées. À la différence du système décimal, un entier apparaissant dans une fraction continue n'est en général pas borné par 9, il peut devenir arbitrairement grand. Alexandre Khintchine s'est intéressé à la moyenne, au sens de limite des moyennes géométriques de tous ces dénominateurs. Pour presque tous les nombres, cette moyenne est la même. Le mot presque possède ici un sens bien particulier. Cette moyenne est appelée constante de Khintchine.
Il est aussi possible de construire des développements en fractions en plaçant les barres de fraction sur le numérateur et non en dessous, on obtient un développement en série d'Engel :