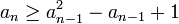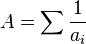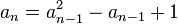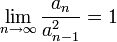Suite de Sylvester - Définition
La liste des auteurs de cet article est disponible ici.
Divisibilité et factorisations
Si i < j, il résulte de la définition que sj ≡ 1 (mod si). Par conséquent, deux termes quelconques de la suite de Sylvester sont premiers entre eux. La suite peut donc servir de preuve à l'assertion "il y a une infinité de nombres premiers", puisqu'un nombre premier donné ne peut diviser qu'un terme de la suite au plus.
Plusieurs travaux ont été consacrés à la factorisation des termes de la suite de Sylvester en nombres premiers, mais il demeure beaucoup d'incertitudes à ce sujet. Par exemple, on ne sait pas si tous les termes de la suite sont sans facteurs carrés, bien que tous les termes connus le soient.
Comme Vardi (1991) l'indique, il est facile de déterminer quel terme (s'il existe) de la suite de Sylvester divise un nombre premier p donné : il suffit de calculer les termes de la suite (modulo p) à l'aide de la définition par récurrence jusqu'à trouver un terme congruent à 0 (modulo p) ou un module répété. À l'aide de cette technique, il a pu trouver que 1166 des trois premiers millions de nombres premiers sont des diviseurs des nombres de Sylvester et qu'aucun d'entre eux n'était élevé au carré. Un résultat de Jones (2006) conclue que la densité des diviseurs premiers de la suite de Sylvester a une densité de 0 dans l'ensemble des nombres premiers.
La table ci-après présente la factorisation des termes de la suite de Sylvester (à l'exception des quatre premiers termes qui sont tous des nombres premiers) :
| n | Factors of sn |
|---|---|
| 4 | 13 × 139 |
| 5 | 3263443, premier |
| 6 | 547 × 607 × 1033 × 31051 |
| 7 | 29881 × 67003 × 9119521 × 6212157481 |
| 8 | 5295435634831 × 31401519357481261 × 77366930214021991992277 |
| 9 | 181 × 1987 × 112374829138729 × 114152531605972711 × P68 |
| 10 | 2287 × 2271427 × 21430986826194127130578627950810640891005487 × P156 |
| 11 | 73 × C416 |
| 12 | 2589377038614498251653 × 2872413602289671035947763837 × C785 |
| 13 | 52387 × 5020387 × 5783021473 × 401472621488821859737 × 287001545675964617409598279 × C1600 |
| 14 | 13999 × 74203 × 9638659 × 57218683 × 10861631274478494529 × C3293 |
| 15 | 17881 × 97822786011310111 × C6649 |
| 16 | 128551 × C13335 |
| 17 | 635263 × 1286773 × 21269959 × C26661 |
| 18 | 50201023123 × 139263586549 × C53339 |
| 19 | C106721 |
| 20 | 352867 × 6210298470888313 × C213419 |
| 21 | 387347773 × 1620516511 × C426863 |
| 22 | 91798039513 × C853750 |
Pn représente un nombre premier connu de n chiffres et Cn un nombre composé de n chiffres dont la décomposition est connue.
Unicité des séries à croissance rapide ayant une limite rationnelle
Sylvester observa lui-même que la suite qui porte son nom semblait posséder la propriété unique d'avoir une croissance extrêmement rapide, alors que la série somme de ses inverses convergeait vers un rationnel.
Plus précisément, il résulte des travaux de Badea (1993) que, si une suite d'entiers an croît suffisant pour que
et si la série
converge vers un rationnel A, alors, pour tout n au-delà d'une certaine valeur, la suite peut être définie par la même relation de réccurence
que la suite de Sylvester.
Erdős (1980) conjectura que pour les résultats de ce type, l'inégalité conditionnant la croissance de la suite pouvait être remplacée par la condition plus faible :