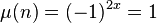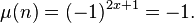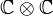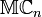Nombre composé - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Propriétés - Sortes de nombres composés - Généralisation aux entiers relatifs

Introduction

Un nombre composé est un entier naturel différent de 0 qui possède un diviseur positif autre que 1 ou lui-même. Par définition, chaque entier plus grand que 1 est donc soit un nombre premier, soit un nombre composé, et les nombres 0 et 1 ne sont ni premiers ni composés.

Par exemple, l'entier 14 est un nombre composé parce qu'il a les nombres 1, 2, 7 et 14 pour diviseurs (quatre diviseurs). Remarquons qu'un carré parfait a toujours un nombre impair de diviseurs (9 a comme diviseurs 1, 3, 9) tandis qu'un entier qui n'est pas un carré parfait a toujours un nombre pair de diviseurs.

Tous les entiers naturels pairs, hormis zéro et deux, sont composés. La méthode permettant de lister tous les entiers naturels impairs composés est appelée crible de Sundaram.

Propriétés

Tous les nombres pairs plus grands que 2 sont composés.
Le plus petit nombre composé est 4.
Chaque nombre composé peut être écrit comme un produit de nombres premiers (non nécessairement distincts).

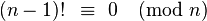
En outre, $(n-1)! \,\,\, \equiv \,\, 0 \pmod{n}$ pour tous les nombres composés n > 5.

Sortes de nombres composés

Une manière de classer les nombres composés consiste à compter le nombre de facteurs premiers. Un nombre composé avec deux facteurs premiers est un nombre semi-premier ou un nombre 2-presque premier (les facteurs n'ont pas besoin d'être distincts, par conséquent, les carrés de nombres premiers sont inclus). Un nombre composé avec trois facteurs premiers distincts est un nombre sphénique. Dans quelques applications, il est nécessaire de différentier les nombres composés d'un nombre impair de facteurs premiers distincts de ceux composés d'un nombre pair de facteurs premiers distincts. Pour ce dernier cas

(où $\mu\,$ est la fonction de Möbius et x est la moitié du total des facteurs premiers), tandis que pour le cas précédent

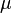
À noter, néanmoins, que pour les nombres premiers, la fonction retourne aussi -1, et que $\mu(1) = 1\,$ . Pour un nombre n avec un ou plus de nombres premiers répétés, $\mu(n) = 0\,$ .

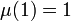
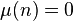
Une autre manière de les classer consiste à compter le nombre de diviseurs. Tous les nombres composés ont au moins trois diviseurs. Dans le cas des carrés de nombres premiers, ces diviseurs sont ${1, p, p 2}$ . Un nombre n qui possède plus de diviseurs qu'un x < n quelconque est un nombre hautement composé (bien que les deux premiers de ces nombres sont 1 et 2).

v · d · m Notion de nombre
Ensembles usuels	$\mathbb{N}$ Entier naturel • $\mathbb{Z}$ Entier relatif • $\mathbb{D}$ Nombre décimal • $\mathbb{Q}$ Nombre rationnel • $\mathbb{R}$ Nombre réel • $\mathbb{C}$ Nombre complexe
Extensions	$\mathbb{H}$ Quaternion • $\mathbb{O}$ Octonion • $\mathbb{S}$ Sédénion • Nombre complexe fendu • Tessarine • $\mathbb{C}\otimes\mathbb{C}\,$ Nombre bicomplexe • $\mathbb{MC}_n$ Nombre multicomplexe • Biquaternion • Coquaternion • Octonion fendu • Nombre hypercomplexe • $\mathbb{Q}_p$ Nombre p-adique • Nombre hyperréel • Nombre superréel • Nombre dual • Droite réelle achevée • Nombre cardinal • Nombre ordinal • Nombre surréel et pseudo-réel
Propriétés particulières	Parité • Nombre premier • Nombre composé • Carré parfait • Nombre parfait • Nombre positif • Nombre négatif • Fraction dyadique • Nombre irrationnel • Nombre algébrique • Nombre transcendant • Nombre imaginaire pur • Nombre de Liouville • Nombre normal • Nombre univers • Nombre constructible • Nombre réel calculable • Nombre transfini • Infiniment petit • Infiniment grand
Exemples d’importance historique	π Pi • √2 Racine carrée de deux • φ Nombre d’or • 0 Zéro • $i$ Unité imaginaire • $e$ Constante de Neper • ℵ₀ Aleph-zéro • Table de constantes mathématiques
Notions connexes	Chiffre • Numération • Fraction • Opération • Calcul • Algèbre • Arithmétique • Suite d’entiers • ∞ Infini • Chiffre significatif