Test de normalité - Définition

Tests bayesien

Kullback-Leibler distances between the whole posterior distributions of the slope and variance do not indicate non-normality. However, the ratio of expectations of these posteriors and the expectation of the ratios give similar results to the Shapiro-Wilk statistic except for very small samples, when non-informative priors are used.

Spiegelhalter suggests using Bayes factors to compare normality with a different class of distributional alternatives. This approach has been extended by Farrell and Rogers-Stewart.

Approche probabiliste

Il existe également un grand nombre de tests de normalité:

• Tests basés sur la fonction de répartition empirique : Test de Kolmogorov-Smirnov et son adaptation le test de Lilliefors (en), ou le test de Anderson-Darling (en) et le test de Cramer–Von Mises (en)

• Tests basés sur les moments, comme le Test de Jarque Bera ou test D'Agostino's K-squared (en)

• Test d'adéquation du χ²

• ou encore le test de Shapiro-Wilk (en), ou le test de Shapiro–Francia.

Généralités

Les tests de normalité sont des tests d'hypothèse. En notant F(x) la fonction de répartition basée sur les données à analyser et F₀(x) la fonction de répartition théorique, les hypothèses nulle et alternative peuvent s'écrire :

.

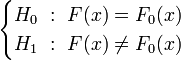
Les tests sur les moments ont une hypothèse moins forte, ils ne testent pas si la fonction de répartition est normale, mais si les moments (coefficients d'asymétrie et d'aplatissement) de la distribution inconnue sont identiques à ceux d'une loi normale:

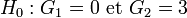
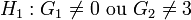
On remarquera que ce n'est pas suffisant pour caractériser une loi normale (Problème des moments).

Test d'adéquation du χ²

Son utilisation n'est pas recommandée du fait de son manque de puissance et de la nécessité de diviser les distributions en classes.

.

Applications

Une application des tests de normalité concerne les résidus d’un modèle de régression linéaire. S’il ne sont pas distribués de façon normale, les résidus ne peuvent pas être utilisés dans des tests Z ou dans quelqu’autre test que ce soit, à partir du moment où il fait intervenir des hypothèses de normalité (par exemple, le test t, le test de Fisher ou le test du χ²). Si les résidus ne sont pas normalement distribués, cela signifie que la variable dépendante, ou tout au moins une variable explicative, pourrait avoir une fonction de répartition erronée ; des variables importantes peuvent également être manquantes. Une ou plusieurs correction de ces erreurs classiques peuvent engendrer des résidus qui suivent une distribution normale.