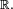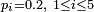Fonction de répartition - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des probabilités ou en statistiques, la fonction de répartition d'une variable aléatoire réelle caractérise la loi de probabilité de cette variable aléatoire réelle. La fonction de répartition de la variable aléatoire réelle
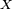
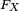

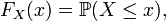
où le membre de droite réprésente la probabilité que la variable aléatoire réelle
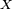
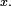
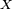
![\ \scriptstyle ]a, b]\](https://static.techno-science.net/illustration/Definitions/autres/d/d222a4a91997a6c8e8e5fd493438dccd_53ef15f74e6a2b5b6adf219bf3fe9bf7.png)
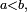
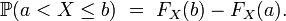
La fonction de répartition d'une mesure de probabilité

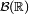
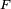

![F(x) = \mathbb{P}(]-\infty, x]).](https://static.techno-science.net/illustration/Definitions/autres/5/57ec4f5b8b6fb7931aa32b030458ef10_95788fb900994c013b69b8a3022b5781.png)
Exemples de calculs de la fonction de répartition
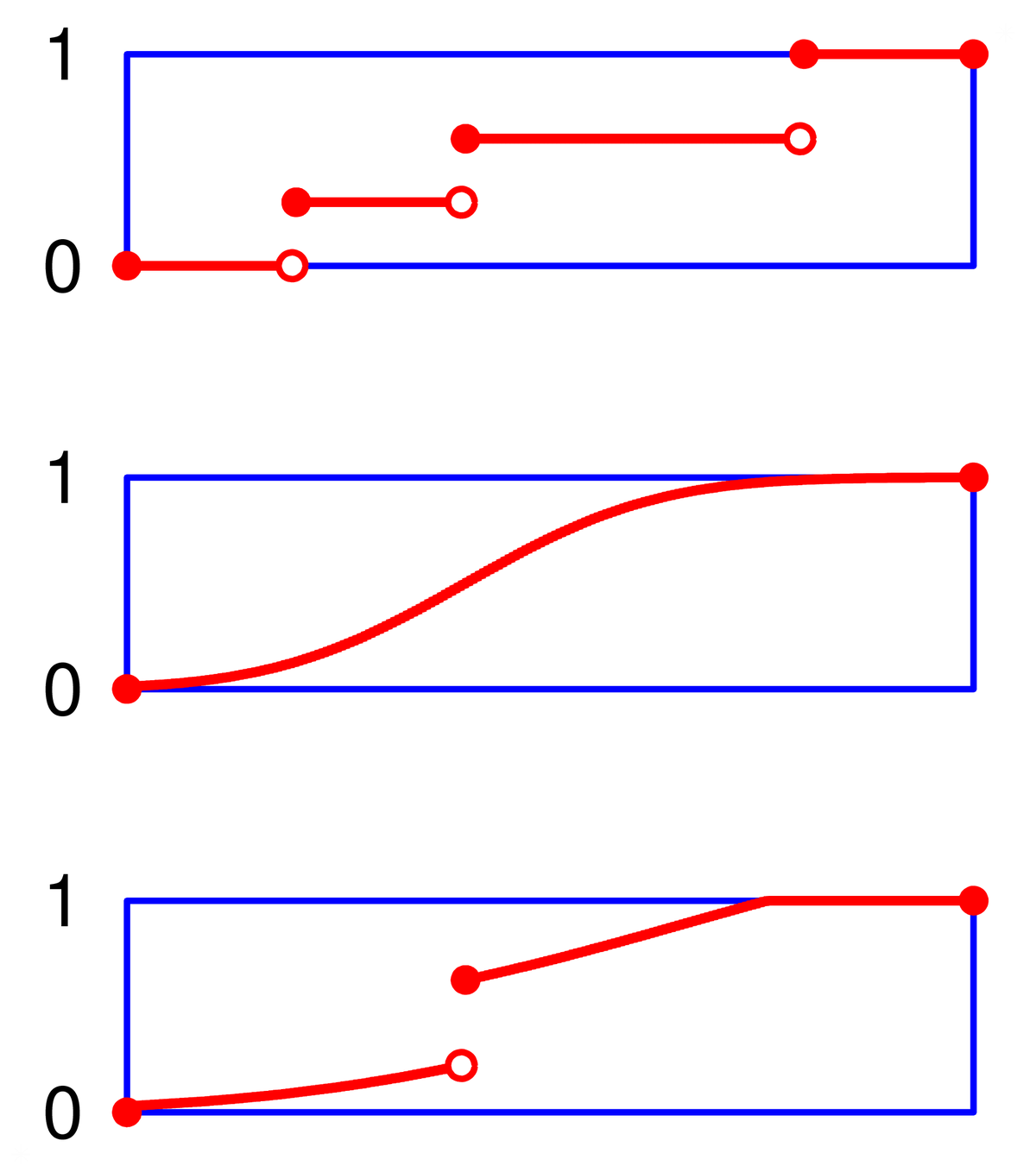
Variables à densité
La fonction de répartition
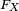

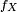
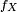
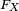
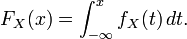
Toutefois, ce n'est pas, en toute généralité, une primitive au sens strict du terme : on peut seulement affirmer
- qu'une fonction de répartition
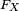
- que si la variable

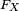
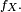
Mais il y a beaucoup de "contre-exemples" : la fonction de répartition de la loi uniforme sur un intervalle, ou encore celle de la loi exponentielle, ne sont pas dérivables sur tout
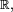
Notons que, contrairement aux variables discrètes, une variable à densité X vérifie

Variables discrètes
Une variable aléatoire
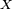

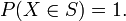
La loi de
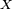
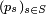
Si, par exemple,
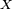
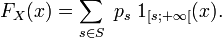
où
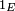
Pour les variables aléatoires discrètes les plus courantes (par exemple, les lois uniformes, binomiales, de Poisson)

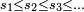
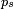
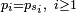
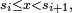
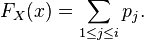
Soit encore, plus généralement :
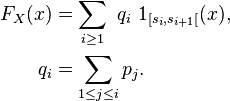
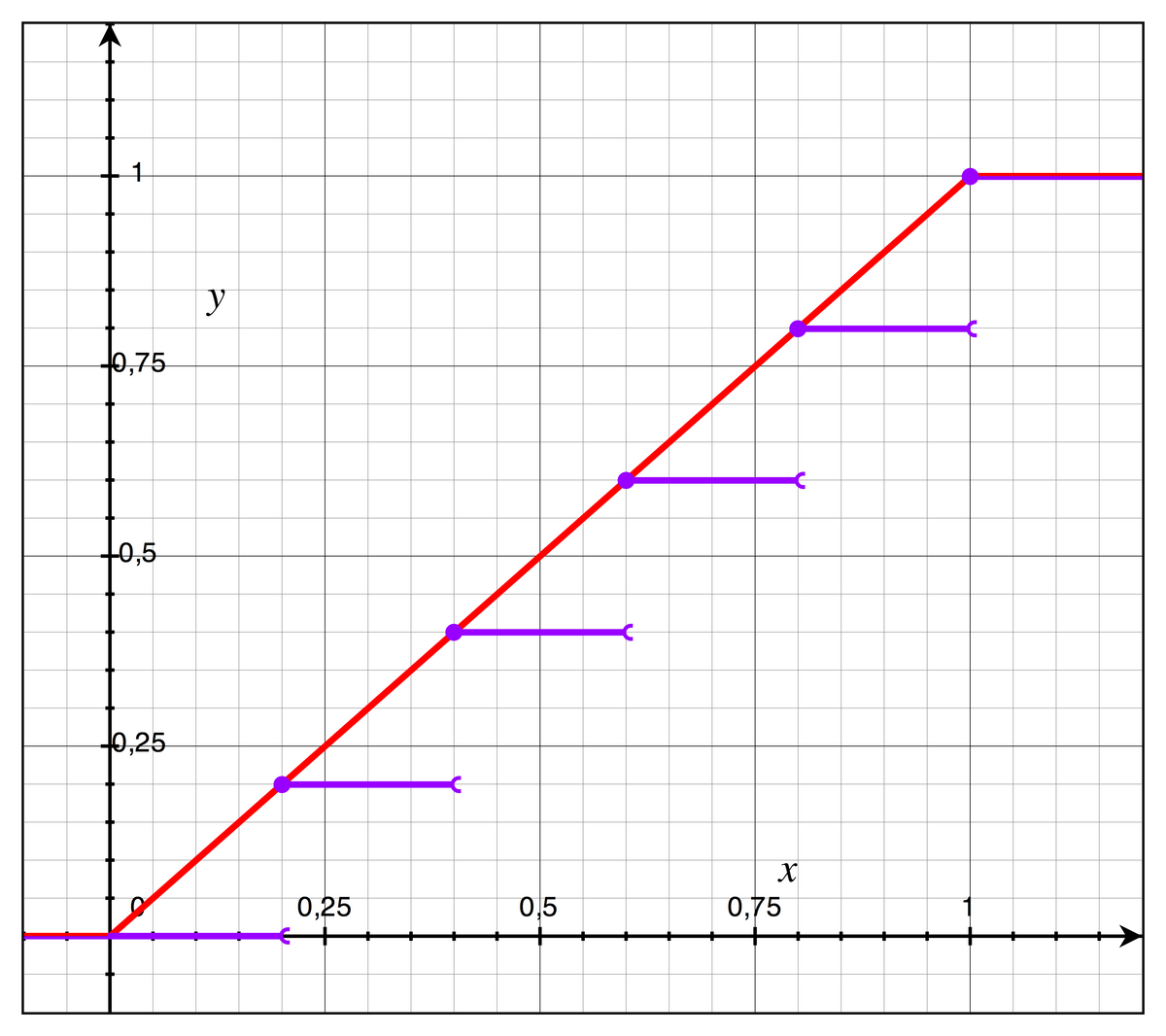
La fonction de répartition est alors une fonction constante par intervalles et sa représentation graphique est en escalier. Les sauts d'une marche à l'autre de l'escalier se situent aux abscisses
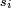

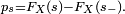
 Voir la section Propriétés de la fonction de répartition pour une démonstration.
Voir la section Propriétés de la fonction de répartition pour une démonstration.
Miscellanées
L'escalier de Cantor F est un exemple de fonction de répartition continue mais dont la dérivée est presque partout nulle. Ainsi, les formules précédentes ne valent pas pour l'escalier de Cantor : pour x>0, on n'a pas
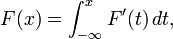
car l'escalier de Cantor F prend des valeurs strictement positives sur
![\scriptstyle\ ]0, +\infty[,\](https://static.techno-science.net/illustration/Definitions/autres/3/3b0863ee7274bace7344868547adc60e_1c8f10afddfcef44c9799d574eae9e66.png)
est de mesure de Lebesgue nulle. Par ailleurs, la loi de probabilité associée à l'escalier de Cantor est diffuse (sans atome), puisque F est une fonction continue sur