Théorème de Lie-Kolchin - Définition
La liste des auteurs de cet article est disponible ici.
Le Théorème de Lie-Kolchin est un résultat de trigonalisabilité des sous-groupes connexes et résolubles du groupe des matrices complexes inversibles
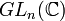
Définition — On dit que
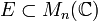
Théorème de Lie-Kolchin — Tout sous groupe connexe résoluble de
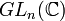
La preuve repose sur les deux lemmes suivants :
Lemme 1 — Soit
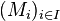
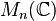
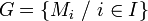
On raisonne par récurrence sur la dimension de l'espace : n.
- Pour n = 1, le résultat est trivial.
- Soit
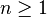
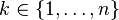
Soit G une famille de matrices qui commutent de
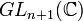
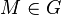
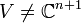
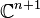
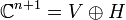
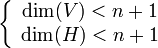
Notons d la dimension de V.
Soit
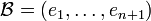
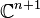
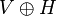
Ainsi dans la base
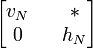
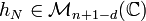
On vérifie que pour N' une matrice de G telle que
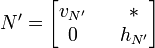
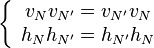
Ainsi, par hypothèse de récurrence, il existe une base
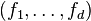
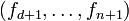
Si on pose
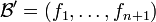
La récurrence est donc établie et le lemme démontré.
Lemme 2 — Si G est un sous-groupe connexe de
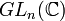
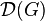
Soit S l'ensemble des commutateurs et
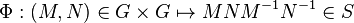
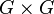
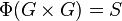
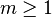
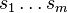
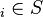
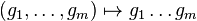
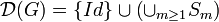
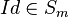
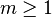
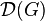
Vient enfin la démonstration du théorème.
Montrons d'abord par récurrence sur n que s'il existe un sous-espace vectoriel propre
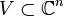
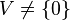
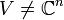
- n = 1 : le résultat est vrai.
- Supposons la propriété démontrée pour tout sous-groupe G connexe et résoluble de
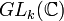
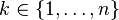
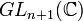
Soit V un sous-espace vectoriel propre de
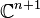
Notons W un supplémentaire de V dans
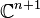
Dans une base adaptée à la décomposition en somme directe, un élément M de G a pour forme :
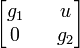
De plus, si d est la dimension de V, les applications :
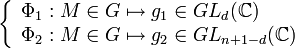
sont continues en tant que projections et sont des morphismes de groupes. Or l'image d'un groupe résoluble par un morphisme de groupe est résoluble. L'image d'un connexe par une application continue étant connexe on peut appliquer l'hypothèse de récurrence à V et W, à savoir qu'il existe une base commune de trigonalisation pour chaque sous espace et en concaténant les deux bases obtenues, on a le résultat pour n + 1.
Ceci achève la démonstration dans le cas où il existe des sous-espaces propres G-stable.
On va maintenant prouver que dans le cas où il n'existe pas de sous-espace propre G-stable, alors G est commutatif, ce qui grâce au lemme démontrera le résultat.
Supposons par l'absurde qu'il existe m > 1 tel que
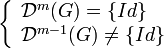
Soit
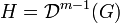
On va montrer qu'en fait l'ensemble H est diagonalisable. Notons
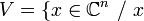
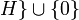
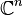
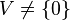
Soit
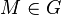
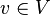
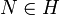
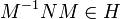
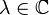
Ainsi, NMv = λMv donc
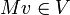
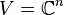
Les éléments de H sont donc diagonalisable dans une base commune.
Montrons alors que
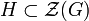
Fixons
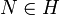
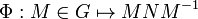
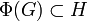
Φ est continue donc Φ(G) est connexe.
De plus, MNM − 1 est diagonalisable car N l'est et a les même valeurs propres que N. Φ(G) a donc un nombre fini d'éléments. Comme Φ(G) est connexe, il n'y en a qu'un d'où Φ(G) = {Φ(Id)} = {N}, ainsi
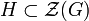
On montre alors que tous les éléments de H sont des homothéties c'est-à-dire que N = λNH. Soit
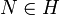
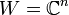
Or
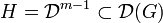
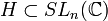
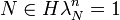
De plus d'après le lemme 2 H est connexe donc H est réduit à un élément donc nécessairement H = {Id}, ce qui est contradictoire. G est donc commutatif, ce qui démontre le théorème.

















































