Variété projective - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie algébrique, les variétés projectives forment une classe importante de variétés. Elles vérifient des propriétés de compacité et des propriétés de finitude. C'est l'objet central de la géométrie algébrique globale.
Sur un corps algébriquement clos, les points d'une variété projective sont les points d'un ensemble algébrique projectif.
Définition
On fixe un corps (commutatif) k.
- Algèbre homogène. Soit B le quotient de
![k[T_0,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/0/00e6a61cac2cd5cba01ea2bd98322bc8_294cfd9cfb599351a65892bf24662aa7.png)
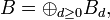
- où Bd est l'ensemble des classes modulo I des polynômes homogènes de degrés d. Les éléments de Bd sont appelés des éléments homogènes de degré d. Un idéal homogène de B est un idéal engendré par des éléments homogènes. Un idéal homogène particulier est B + , ensemble des éléments homogènes de degré strictement positif. C'est l'idéal maximal engendré par les classes des
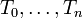
- Espace topologique. Par définition, l'ensemble Proj B est constitué des idéaux premiers homogènes de B ne contenant pas B + (donc strictement contenus dans B + ) et maximaux pour cette propriété. Pour tout idéal homogène I, on note V + (I) l'ensemble des idéaux premiers q dans Proj B contenant I. Lorsque l'on fait varier les I, les parties V + (I) de ProjB constituent les parties fermées de la topologie de Zariski sur Proj B.
- Une base de topologie. Si f est un élément homogène, on note D + (f) le complémentaire de V + (fB). C'est un ouvert principal. Les ouverts principaux constituent une base de topologie. De plus, l'espace topologique D + (f) est homéomorphe au spectre maximal Spm(B(f)), où B(f) est l'ensemble des éléments de la localisation Bf qui peuvent être représentés par une fraction b / fm avec b homogène de degré mdegf. L'algèbre B(f) est de type fini sur k.
- Proposition. Il existe une unique structure de variété algébrique sur ProjB telle que pour tout f homogène, la sous-variété ouverte D + (f) soit isomorphe à la variété algébrique affine SpmB(f).
- Définition. Une variété projective sur k est une variété algébrique sur k isomorphe à ProjB pour une k-algèbre homogène B.
- Une variété quasi-projective est une sous-variété ouverte d'une variété projective. Toute variété affine se plonge comme sous-variété ouverte dans une variété projective. Ainsi toute variété quasi-affine est quasi-projective.
Propriétés
- Si B est une algèbre homogène, quotient de
![k[T_0,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/0/00e6a61cac2cd5cba01ea2bd98322bc8_294cfd9cfb599351a65892bf24662aa7.png)
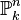
- Le produit de deux variétés projectives est une variété projective. Cela résulte du plongement de Segre qui identifie le produit
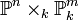
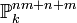
- Toute variété projective est séparée, et propre sur k.
- Si
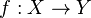
- Si
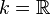
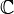
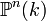
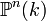
- Pour l'espace projectif
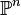
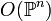
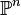
- Il en résulte qu'une variété projective qui est aussi affine est nécessairement constituée d'un nombre fini de points (i.e. de dimension 0).

















































