Variété algébrique affine - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie algébrique, une variété affine est un modèle local pour les variétés algébriques, c'est-à-dire que celles-ci sont obtenues par recollement de variétés affines.
Origine
Points de vue analytique et algébrique
Le point de vue le plus simple pour décrire une variété algébrique affine est l'ensemble des solutions d'un système d'équations polynomiales à coefficients dans un corps commutatif K. Autrement dit une variété affine est une partie de Kn dont les points annulent des polynômes P1, ...,Pr de K[X1, ...,Xn]. La géométrie algébrique offre une vision purement algébrique de ce concept de variété affine, par l'équivalence suivante :
![\left\{\begin{array}{l} P_1(x_1,\dots,x_n)=0 \\ \vdots \\P_r(x_1,\dots,x_n)=0 \end{array} \right. \quad \equiv \quad \text{Spm } \frac{\mathbb{K}[X_1,\dots,X_n]}{\sqrt{I(P_1,\dots,P_r)}}](https://static.techno-science.net/illustration/Definitions/autres/1/12342ee250e65793942df2fee1f005cb_7f9895d2074f6dec28d6e044b86bc88a.png)
avec Spm le spectre maximal (ie l'ensemble des idéaux maximaux), I l'idéal engendré et √ le radical d'un idéal.
Le point de vue de gauche est dit analytique et celui de droite algébrique. Dans le point de vue algébrique on ne manipule plus des points de Kn mais des polynômes à n indéterminées.
Exemples
- L'ensemble Kn est une variété algébrique affine (lieu d'annulation du polynôme nul), il correspond à Spm K[X1, ...,Xn] entier.
- Le cercle x² + y² = 1 dans ℝ² est une variété affine, de même que les coniques.
Explication de la correspondance ≡
On note A = K[X1, ...,Xn] / √( I(P1, ...,Pr) ) la K-algèbre quotient de polynômes servant à définir la variété affine.
Ce quotient permet d'écrire Pi (X1, ...,Xn) = 0 en remplaçant les petits xj ∈ K par des grands Xj indéterminés. On peut donc formellement effectuer les mêmes calculs sur les Xj que sur les xj.
Le radical d'idéal autorise les simplifications de la forme
avec Q un polynôme et m entier positif, à l'instar de ce qui se passerait en travaillant avec les petits xj ∈ K. Autrement dit A est une K-algèbre réduite, au sens où son seul élément nilpotent est 0.
L'opération Spm sert à extraire de A un ensemble que l'on a envie d'identifier avec Z(I(P1, ...,Pr)) ⊂ Kn, l'intersection des zéros de tous les Pi, c'est-à-dire la variété du point de vue anaytique. On a en effet l'injection canonique suivante
avec π la projection canonique dans l'anneau quotient. Si de surcroît le corps K est algébriquement clos, le nullstellensatz prouve que cette injection est une bijection. Lorsque K n'est pas algébriquement clos, le spectre maximal peut être un peu plus gros que l'ensemble des zéros dans Kn, mais ce n'est pas gênant en pratique. On peut s'en convaincre sur des exemples simples de variétés affines.
Une information sur la variété affine est codée dans l'intégrité de A. Considérons notamment la variété affine réelle (x-1)(x-2) = 0. Par intégrité dans les réels, on déduit immédiatement que x=1 ou x=2, ce qui fait que la variété a 2 points. On vérifie que Spm A a également 2 points, comme il se doit. En revanche on ne peut ni écrire X=1 ni X=2 dans les polynômes, car chacun réduirait la variété à 1 point, A n'est donc pas intègre ici. Il vient qu'une variété affine est faite d'un seul morceau si et seulement si son algèbre quotient A est intègre, ie √( I(P1, ...,Pr) ) est un idéal premier. On dit dans ce cas que la variété est irréductible.
On remarque enfin que A est une K-algèbre de type fini ; le reste de cet article est donc consacré à la structure des spectres maximaux de ces algèbres. On verra que ce sont des espaces topologiques localement annelés.
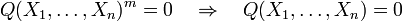
![\begin{array}{rcl} \phi : Z(I(P_1,\dots,P_r)) &\to &\text{Spm } \frac{\mathbb{K}[X_1,\dots,X_n]}{\sqrt{I(P_1,\dots,P_r)}} \\ (a_1, \dots,a_n)&\mapsto & \pi(\, I(X_1-a_1,\dots ,X_n-a_n)\, )\end{array}](https://static.techno-science.net/illustration/Definitions/autres/1/1744b795e59125164fbbf096b738a9be_dc86f969fe6d91fb7c3e4fbb66338d08.png)

















































