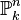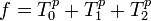Variété projective - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Exemples
- La variété projective s'appelle l'espace projectif de dimension n sur k. On note cette variété
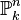
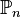
![k[X_1,\ldots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
![k[X_1,\ldots, X_n]](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
- Si f est un polynôme homogène à n + 1 variables et non-nul. Alors
![{\rm Proj} (k[T_0,\ldots, T_n]/(f))](https://static.techno-science.net/illustration/Definitions/autres/f/f5485064df5780ae813eb5735b77ba07_fb9364f05b1f972865b4b5d676110766.png)
![{\rm Proj} (k[T_0,\ldots, T_n]/(f))](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f5485064df5780ae813eb5735b77ba07_fb9364f05b1f972865b4b5d676110766.png)
