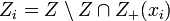Ensemble algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie algébrique, les ensembles algébriques sont, grosso modo, les points d'une variété algébrique affine ou projective. Ils servent de support intuitif à la géométrie algébrique.
Ensembles algébriques affines
Dans cette section k désignera un corps algébriquement clos (par exemple ℂ), n un entier supérieur ou égal à un. On considère l'espace affine de dimension n sur k, c’est-à-dire l'ensemble kn (dépourvu de structure algébrique).
Définition. Soit S une partie de l'anneau des polynômes
![k[X_1,\ldots,X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
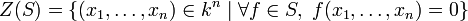
c’est-à-dire le lieu d'annulation commun à tous les éléments de S.
Remarques
- Si I est l'idéal de
![k[X_1,\ldots,X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
![k[X_1,\ldots,X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
- Etant donné un ensemble algébrique
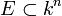
![k[X_1,\ldots,X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
- Comme k est algébriquement clos, le théorème des zéros de Hilbert affirme que la fonction I est une bijection entre les ensembles algébriques de kn et les idéaux radiciels de
![k[X_1,\ldots,X_n]](https://static.techno-science.net/illustration/Definitions/autres/c/c901657f34686cd7c6d58c0019836751_d7df041ba679369e40a6a5f082399992.png)
![k[X_1,\ldots,X_n]/I(E)](https://static.techno-science.net/illustration/Definitions/autres/2/2234cae864a4459c42bc48abac3e9dc5_6bca1a536b63b3c6a145eac5ad1f44da.png)
- Un ensemble algébrique E est dit irréductible ssi I(E) est un idéal premier.
Exemples :
- Dans le plan affine k2, le lieu d'annulation d'un polynôme à deux variables non-nul est un ensemble algébrique affine appelé courbe plane et le degré du polynôme est appelé degré de la courbe. Les droites sont les ensembles algébriques de degré 1, les coniques ceux de degré 2, les cubiques ceux de degré 3 et ainsi de suite.
- Dans l'espace affine k3 le lieu d'annulation d'un polynôme à trois variables non-nul est un ensemble algébrique affine qui est une surface algébrique . Tout comme pour les courbes on définit le degré d'une surface, les plans sont de degré 1, les quadriques de degré 2 etc.
- Dans un espace affine, tout ensemble fini de points est un ensemble algébrique affine.
Propriétés:
- Z({0}) = kn, Z({1}) est vide;
-
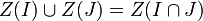
- L'intersection d'une famille d'ensembles algébriques Z(Iλ) est égale à Z(I), où I est l'idéal engendré par
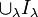
Topologie de Zariski
L'espace affine kn (resp. projectif Pn(k)) est muni d'une topologie dite de Zariski. Les parties fermées pour cette topologie sont les ensembles algébriques dans kn (resp. ensembles algébriques projectifs dans Pn(k)). La topologie de Zariski sur un ensemble algébrique (resp. ensemble algébrique projectif) est par définition la topologie induite par celle de l'espace affine (resp. projectif) qui le contient.
Les parties ouvertes remarquables de l'espace affine (resp. projectif) sont les ouverts principaux D(f) (resp. D + (f)), c'est-à-dire le complémentaire de Z({f}) (resp. Z + ({f})). La restriction d'un ouvert principal à un ensemble algébrique est appelé ouvert principal de l'ensemble algébrique. Les ouverts principaux forment une base de topologie.
Un sous-ensemble ouvert d'un ensemble algébrique affine (resp. projectif) est appelé quasi-affine (resp. quasi-projectif).
L'espace affine kn est quasi-projectif car il s'identifie à l'ouvert Pn(k) − Z + (X0) de Pn(k) par l'application
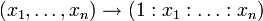
Exemple: Les parties fermées de la droite affine k sont les parties finies et k lui-même.
La topologie de Zariski est apparemment assez pauvre (peu d'ouverts, deux points ne sont en général pas séparés par des voisinages ouverts disjoints), mais elle est suffisante pour beaucoup de propos.
Relations entre ensembles algébriques affines et ensembles algébriques projectifs : Un ensemble algébrique projectif Z est réunion finie d'ouverts (pour sa topologie de Zariski) qui sont des ensembles algébriques affines. En effet, Z est défini par l'annulation de polynômes homogènes à n+1 variables. Notons Zi l'ensemble des