Fonction chi de Legendre - Définition
En mathématiques, la fonction chi de Legendre est définie par
La transformée discrète de Fourier de la fonction chi de Legendre en respectant l'ordre n est la fonction zeta d'Hurwitz (Cvijovic).
La fonction chi de Legendre est un cas particulier de la fonction transcendante de Lerch, et est donnée par
-
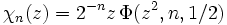
Publication en langue anglaise
- Djurdje Cvijovic and Jacek Klinowski. Math. Comp. 68 (1999), 1623-1630, 1999. (abstract)

















































