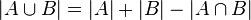Formule du crible de Poincaré - Définition
En combinatoire, la formule du crible de Poincaré ou formule de Poincaré, appelée aussi formule du crible est une relation entre le cardinal d'une réunion d'un nombre fini d'ensembles et les cardinaux de leurs intersections.
Théorème
Soient A1, ..., An n ensembles finis. Nous avons
où |A| désigne le cardinal d'un ensemble fini A.
Cette formule peut aussi s'écrire de façon plus condensée
-
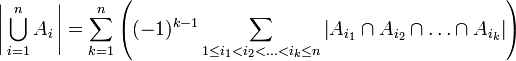
Elle peut se démontrer par récurrence sur n, ou en utilisant les fonctions indicatrices.
Cas particulier
Considérons par exemple, le cas n = 2. Soient A et B deux ensembles finis, la formule s'écrit
où |A| et |B| représentent les cardinaux respectifs de A et B.
En d’autres termes, nous pouvons compter les éléments de la réunion de deux ensembles A et B en additionnant les cardinaux de ces deux ensembles et en soustrayant le cardinal de leur intersection.
Le principe est basé sur une inclusion généreuse, suivie d'une exclusion compensatrice (principe d'inclusion exclusion de Moivre.)
Quand n > 2, l'exclusion des cardinaux des intersections de paires d'ensembles est trop forte (en général), et est corrigée par l'addition et la soustraction de cardinaux d'un nombre supérieur d'ensembles, d'où l'alternance de signes dans la formule générale.
Applications
L'application la plus connue de la formule du crible est sans doute, en combinatoire, la détermination du nombre de dérangements d'un ensemble fini.
Un dérangement d'un ensemble A est une bijection de A sur lui-même sans point fixe.
Grâce au principe d'inclusion-exclusion de Moivre, nous pouvons prouver que si le cardinal de A est égal à n, alors le nombre de dérangements de A est le nombre entier le plus proche de
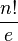
Il s'ensuit que si toutes les bijections ont la même probabilité d'être choisies, alors la probabilité pour qu'une bijection prise au hasard soit un dérangement tend rapidement vers 1/e lorsque n tend vers l'infini.
Dans beaucoup de cas (en particulier, dans le comptage des nombres premiers inférieurs à un entier donné grâce au crible d'Ératosthène), la formule de Poincaré n'est pas d'une grande utilité parce que le nombre de termes qu'elle comporte s'avère excessif. Si chacun des termes de la somme peut être évalué de façon exacte, une accumulation des erreurs de calcul dans les additions peut rendre la formule inapplicable.
En théorie des nombres, cette difficulté fut soulevée par Viggo Brun. Beaucoup plus tard, ses idées furent reprises par d'autres mathématiciens, et de nombreuses variétés de méthodes du crible furent développées. Par exemple, certaines d'entre elles permettent d'encadrer très finement les cardinaux d'ensembles " criblés ", plutôt que de donner une valeur exacte avec une formule trop lourde. De tels encadrements s'obtiennent en remarquant que la somme des premiers termes de la formule du crible est alternativement un majorant et un minorant du cardinal de la réunion.