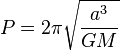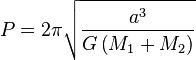Période orbitale - Définition
En astronomie, la période orbitale désigne la durée mise par un astre (étoile, planète, astéroïde) pour effectuer une orbite complète. Par exemple, la Terre a une période orbitale de 365,25 jours.
Si cette rotation est par rapport au Soleil telle que observée sur Terre, on parle de période synodique; c'est la période orbitale apparente. Si elle est relative au étoiles, on parle de période sidérale; cette dernière est considérée comme la période de rotation réelle de l'objet.
Il existe d'autres types de périodes orbitales:
- la période anomalistique est la durée entre deux passages de l'objet à son périastre; selon que ce dernier précesse ou récesse, cette période sera plus courte ou longue que la période sidérale;
- la période draconitique est la durée entre deux passages de l'objet à son nœud ascendant ou descendant, elle dépendra donc des précessions des deux plans impliqués (l'orbite de l'objet et le plan de référence, généralement l'écliptique);
- la période tropique est la durée entre deux passages de l'objet à l'ascension droite zéro; à cause de la précession des équinoxes, cette période est légèrement et systématiquement plus courte que la péride sidérale.
Calculs
Corps orbitant de masse négligeable
La période orbitale
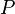
où:
-

-

-

Deux corps
Lorsque l'on tient compte de la masse des deux corps, la période orbitale
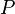
où:
-

-
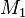
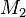
-

On peut noter que la période orbitale est indépendante de la taille.