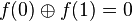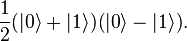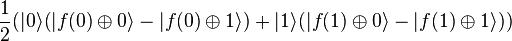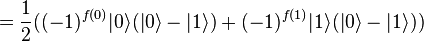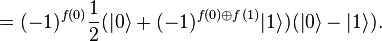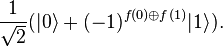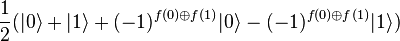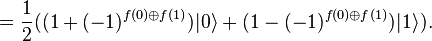Algorithme de Deutsch-Jozsa - Définition

Introduction

L'Algorithme de Deutsch-Jozsa est un algorithme quantique, proposé par David Deutsch et Richard Jozsa en 1992 avec des améliorations de R. Cleve, A. Ekert, C. Macchiavello, et M. Mosca en 1998. Bien qu'il ne soit pas d'un grand intérêt pratique, il s'agit d'un des premiers algorithmes quantiques qui est plus efficace qu'un algorithme classique.

Le problème

Dans le cas du problème de Deutsch-Jozsa, nous disposons d'une boîte noire quantique, connu sous le nom d'Oracle qui implémente une fonction mathématique . Nous savons que cette fonction est soit constante (0 ou 1 sur toutes les entrées) soit équilibrée (0 dans la moitié des cas, 1 dans les autres). Le but du problème est de savoir si la fonction est constante ou équilibrée à l'aide de l'oracle

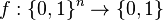
Histoire

L'algorithme est basé sur des travaux de David Deutsch, datant de 1985, concernant le cas n = 1. La question était de savoir si une fonction booléenne, , était constante.

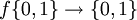
En 1992, l'idée a été généralisée pour pouvoir être appliquée sur un nombre n bits en entrée et savoir si la fonction était constante ou équilibrée.

L'algorithme de Deutsch n'était pas, à l'origine, déterministe. L'algorithme retournait une réponse juste avec une probabilité de 50%. L'algorithme original de Deutsch-Jozsa était déterministe, mais, à la différence de l'algorithme de Deutsch, il nécessitait deux évaluations de la fonction.

Plusieurs améliorations ont été apportées à l'algorithme de Deutsch-Jozsa par Cleve et al qui ont résulté en un algorithme qui est déterministe et ne nécessite qu'une seule évaluation de la fonction f. Cet algorithme est appelé l'algorithme de Deutsch-Josza en l'honneur de l'importance des techniques qui ont été utilisées.

L'algorithme de Deutsch-Jozsa a servi d'inspiration pour les algorithme de Shor et de Grover, deux des algorithmes quantiques les plus révolutionnaires.

La solution classique

Si un algorithme classique et déterministe est utilisé, il faut 2^{n − 1} + 1 évaluation de la fonction mathématique f dans le pire des cas pour trouver la solution.

Dans le cas de l'utilisation d'un algorithme probabiliste, un nombre constant d'évaluation est suffisant pour trouver la bonne réponse avec une forte probabilité, néanmoins 2^{n − 1} + 1 évaluation sont toujours nécessaire pour que la réponse soit toujours correcte. L'algorithme quantique de Deutsch-Jozsa permet de trouver une réponse toujours correcte avec une seule évaluation de f.

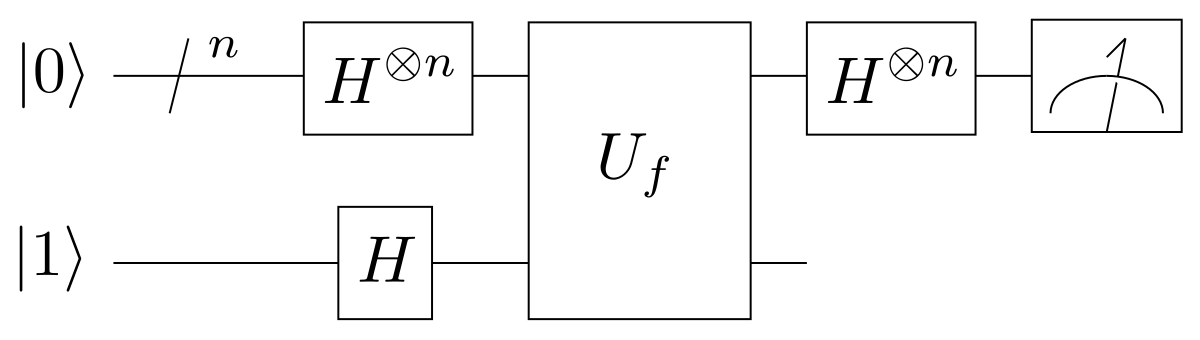
L'algorithme de Deutsch-Jozsa, en détail

Le circut quantique de l'algorithme de Deutsch-Jozsa

Nous commençons avec le n+1 bit dans l'état . Les premiers n bits sont tous dans l'état et les derniers bit dans l'état . Nous appliquons ensuite la transformation d'Hadamard à chaque qubit, pour obtenir

.

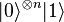
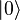
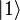
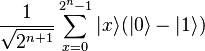
L'Algorithme de Deutsch-Jozsa est un algorithme quantique, proposé par David Deutsch et Richard Jozsa en 1992 avec des améliorations de R. Cleve, A. Ekert, C. Macchiavello, et M. Mosca en 1998. Bien qu'il ne soit pas d'un grand intérêt pratique, il s'agit d'un des premiers algorithmes quantiques qui est plus efficace qu'un algorithme classique.

Algorithme de Deutsch, un cas spécial

Le but est de tester la condition f(0) = f(1) ; Cela est équivalent à vérifier . Si cela vaut zéro alors f est constante, sinon f est équilibrée.

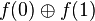
L'algorithme commence avec deux qubit dans l'état . Une transformation d'Hadamard est d'abord appliquée à chaque qubit. Cela donne

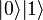
Une implémentation quantique (oracle) de la fonction f permet de passer de à . En appliquant cette fonction à notre état, nous obtenons

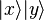
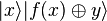
Nous ignorons le dernier bit and la phase and alors nous avons l'état

En appliquant une transformation d'hadamard à cet état, nous obtenons

si et seulement si nous observons un zéro. Donc, la fonction est constante si et seulement si nous mesurons un zéro.