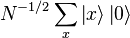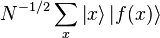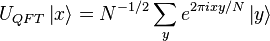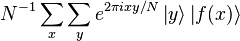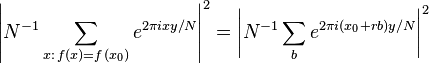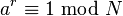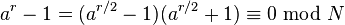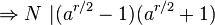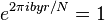Algorithme de Shor - Définition

Introduction

En arithmétique modulaire, l’algorithme de Shor est un algorithme quantique pour factoriser un nombre N en temps O((logN)³) et en espace O(logN), nommé en l'honneur de Peter Shor.

Beaucoup de cryptosystèmes à clé publique, tels que le RSA, deviendraient vulnérables si l'algorithme de Shor était un jour implémenté dans un calculateur quantique pratique. Un message chiffré avec RSA peut être déchiffré par factorisation de sa clé publique N, qui est le produit de deux nombres premiers. En l'état actuel des connaissances, il n'existe pas d'algorithme classique capable de faire cela en temps O((logN)^k) pour n'importe quel k, donc, les algorithmes classiques connus deviennent rapidement impraticables quand N augmente, à la différence de l'algorithme de Shor qui peut casser le RSA en temps polynomial. Il a été aussi étendu pour attaquer beaucoup d'autres cryptosystèmes à clé publique.

Comme tous les algorithmes pour calculateur quantique, l'algorithme de Shor est probabiliste : il donne la réponse correcte avec une haute probabilité et la probabilité d'échec peut être diminuée en répétant l'algorithme.

L'algorithme de Shor fut utilisé en 2001 par un groupe d'IBM, qui factorisa 15 en 3 et 5, en utilisant un calculateur quantique de 7 qubits.

Procédure

Le problème que nous allons essayer de résoudre est le suivant, soit un entier donné N, nous essayons de trouver un autre entier p compris entre 1 et N qui divise N.

L'algorithme de Shor consiste en deux parties :

1. Une réduction du problème de factorisation en un problème de recherche d'ordre, qui peut être effectué sur un ordinateur classique.
2. Un algorithme quantique pour résoudre le problème de recherche d'ordre.

Partie classique

1. Prendre un nombre pseudo-aléatoire a < N
2. Calculer le PGCD(a, N). Ceci peut être effectué par l'utilisation de l'algorithme d'Euclide.
3. Si PGCD(a, N) ≠ 1, alors c'est un facteur non-trivial de N, donc effectué.
4. Autrement, utiliser la sous-routine de recherche de période (ci-dessous) pour trouver r, la période de la fonction suivante :
   ,
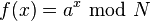
   c.a.d. le plus petit entier r pour lequel f(x + r) = f(x).
5. Si r est impair, retourner à l'étape 1.
6. Si a ^r/2 ≡ -1 (mod N), retourner à l'étape 1.
7. Les facteurs de N sont PGCD(a^r/2 ± 1, N). Effectué.

Partie quantique : sous-routine de recherche de période

1. Commencer avec des registres d'entrée et de sortie de chacun log₂N qubits, et les initialiser à:

   

   où x va de 0 à N - 1.

2. Construire f(x) comme une fonction quantique et l'appliquer à l'état précédent, pour obtenir

   

3. Appliquer la transformée de Fourier quantique au registre d'entrée. La transformée de Fourier quantique sur N points est définie par :

   

   Ce qui donne l'état suivant :

   

4. Effectuer une mesure. On obtient ainsi une certaine valeur y dans le registre d'entrée et f(x₀) dans le registre de sortie. Comme f est périodique, la probabilité de mesurer un certain y est donnée par

   

   Le calcul montre que cette probabilité est plus haute quand yr/N est proche d'un entier.

5. Mettre y/N sous forme irréductible, et extraire le dénominateur r′, qui est un candidat pour r.
6. Vérifier si f(x) = f(x + r′). Si c'est le cas, c'est terminé.
7. Autrement, obtenir plus de candidats pour r en utilisant des valeurs proches de y, ou multiples de r′. Si un autre candidat marche, c'est terminé.
8. Sinon, retourner à l'étape 1 de la sous-routine.

Explication de l'algorithme

L'algorithme est composé de deux parties. La première partie transforme le problème de factorisation en un problème de recherche de période d'une fonction et peut être implémentée de façon classique. La seconde partie trouve la période en utilisant la transformée de Fourier quantique et est responsable de l'accélération quantique.

I. Obtenir des facteurs à partir de la période

Les entiers inférieurs à N et premiers avec N forment un groupe fini muni de la multiplication modulo N, qui est typiquement noté (Z/NZ)^×. Par la fin de l'étape 3, nous avons un entier a dans ce groupe. Comme le groupe est fini, a doit avoir un ordre fini r, le plus petit entier positif tel que

Par conséquent, N | (a ^r - 1). Supposons que nous sommes capable d'obtenir r et qu'il est pair. Alors

r est le plus petit entier positif tel que N divise (a ^r- 1), donc N ne peut pas diviser (a ^{r / 2} - 1). Si N ne divise pas non plus (a ^{r / 2} + 1), alors N doit avoir un facteur commun non-trivial avec chacun des (a ^{r / 2} - 1) et (a ^{r / 2} + 1).

Preuve : Pour simplifier, notons (a ^{r / 2} - 1) et (a ^{r / 2} + 1) par u et v respectivement. N | uv, donc kN = uv pour certain entier k. Supposons que PGCD(u, N) = 1; alors mu + nN = 1 pour certains entiers m et n (ceci est une propriété du PGCD.) En multipliant les deux côtés par v, nous trouvons que mkN + nvN = v, donc N | v. Par contradiction, PGCD(u, N) ≠ 1. Par un argument similaire, PGCD(v, N) ≠ 1.

Ceci nous fournit une factorisation de N. Si N est le produit de deux nombres premiers, ceci est la seule factorisation possible.

II. Trouver la période

L'algorithme de recherche de période de Shor est fortement relié à la capacité d'un calculateur quantique d'être dans de nombreux états simultanément. Les physiciens appellent ce comportement une « superposition » d'états. Pour calculer la période d'une fonction f, nous évaluons la fonction en tous ses points simultanément.

Pourtant, la physique quantique ne nous permet pas d'accéder à toute l'information directement. Une mesure fournira seulement une parmi toutes les valeurs possibles en détruisant toutes les autres. Par conséquent nous avons à transformer avec précaution la superposition en un autre état qui retournera la réponse correcte avec une haute probabilité. Ceci est achevé par la transformée de Fourier quantique.

Shor eut ainsi à résoudre trois problèmes d'« implémentation ». Tous ont été implémentés « rapidement », ce qui veut dire qu'ils peuvent être implémentés avec un nombre de portes quantiques qui est polynomial en logN.

1. Créer une superposition d'états. Ceci peut être fait en appliquant des portes d'Hadamard à tous les qubits dans le registre d'entrée. Une autre approche serait d'utiliser la transformée de Fourier quantique (voir ci-dessous).
2. Implémenter la fonction f comme une transformation quantique. Pour achever cela, Shor utilisa l'élévation au carré pour sa transformation d'exponentiation modulaire.
3. Exécuter une transformation de Fourier quantique. En utilisant les portes NON contrôlées et les portes qubit à rotation unique Shor conçu un circuit pour la transformée de Fourier quantique qui utilise juste O((logN)²) portes.

Après toutes ces transformations, une mesure fournira une approximation de la période r. Pour simplifier, assurons-nous qu'il existe un y tel que yr/N soit un entier. Alors la probabilité de mesurer y est 1. Pour voir cela, notons qu'alors

Pour tous les entiers b. Par conséquent, la somme qui nous donne la probabilité de mesurer y sera de N/r comme b prend globalement N/r valeurs et ainsi, la probabilité est 1/r. Il existe r y tels que yr/N soit un entier donc les probabilités totalisent 1.

Note : une autre manière d'expliquer l'algorithme de Shor est de noter que c'est juste l'algorithme d'estimation de phase quantique déguisé.