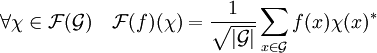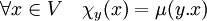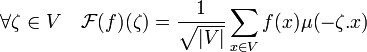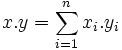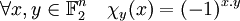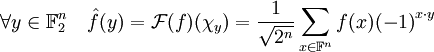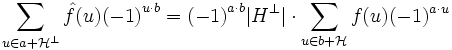Fonction booléenne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une fonction booléenne est une fonction de
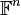
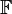
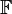
En fait, les fonctions booléennes sont simplement un autre nom des fonctions logiques. Toutefois, lorsque l'on s'attache aux propriétés algébriques de ces fonctions, l'appellation fonction booléenne est la plus utilisée.
Les fonctions booléennes, ou plus précisément leurs propriétés, interviennent notamment en cryptologie dans les boîtes-S, ainsi que dans les chiffrements par flot -- fonction de filtrage ou de combinaison des registres à décalage.
Propriétés
Forme algébrique normale
Les corps finis et les polynômes interpolateurs de Lagrange conduisent rapidement à une propriété fondamentale des fonctions booléennes : la représentation dite « forme algébrique normale » (algebraic normal form ou ANF). Toute fonction booléenne peut s'écrire comme un polynôme en n variables à coefficients dans
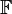
![\mathbb{F}[X_0,...,X_{n-1}]](https://static.techno-science.net/illustration/Definitions/autres/6/6c14262403a85652853ea207a0b73a73_e5dce23b4d11b6f51586c07e967f8327.png)
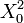
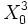
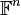
Autrement dit, une fonction booléenne peut être représentée de manière unique par un polynôme de la forme :
On pose fréquemment
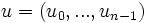
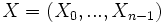
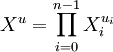
-
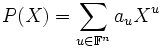
La notion de degré d'une fonction booléenne est alors évidente, il s'agit du degré maximal des monômes de son ANF.
Linéarité et Non-linéarité
Les fonctions de degré 1 sont appelées les fonctions affines. En fait, ce sont des formes affines de l'espace vectoriel
Les cryptographes utilisent le terme de non-linéarité pour parler de la distance d'une fonction booléenne à l'ensemble
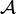
L'intérêt de cette notion est de quantifier l'erreur commise si on remplace la fonction f par une fonction affine : dans le meilleur des cas, on se « trompe »
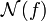
On montre, en utilisant la transformée de Fourier, que la non-linéarité d'une fonction booléenne est au plus de
Lorsque n est pair, cette borne supérieure est atteinte, on parle alors de fonction courbe.
Précisons que l'ensemble des fonctions affines a une importance particulière en théorie des codes correcteurs, au point qu'il possède un nom, le code de Reed-Muller d'ordre 1 (en n variables). L'ordre est le degré maximal des fonctions. Ainsi, le code de Reed-Muller d'ordre

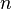
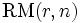
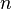

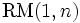
Outil d'étude : la transformée de Fourier
La transformation de Fourier, appliquée aux fonctions booléennes, se révèle être un moyen très puissant pour explorer les différentes propriétés de ces objets. Elle est, par exemple, fréquemment utilisée pour étudier des propriétés cryptographiques comme la non-linéarité maximale. On la retrouve également dans des aspects plus appliquées : l'existence d'algorithmes de calcul de la transformée de Fourier de type FFT sert à décoder efficacement les codes de Reed et Muller. On trouvera dans la suite une présentation générale de la transformation de Fourier dans le cas des groupes abéliens finis qui est ensuite particularisée pour le cas des fonctions booléennes.
Cas d'un groupe abélien fini
Dans le cas d'un groupe abélien fini, le théorème de Kronecker assure que le groupe est isomorphe à un produit direct de groupes cycliques. Ce théorème est à la base de nombreuses propriétés des fonctions booléennes.
Caractère et groupe dual
De manière générale, on peut définir une transformation de Fourier sur un groupe
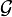
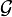
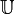

L'ensemble des caractères opèrent sur l'ensemble des applications de
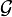

![\mathbb C[\mathcal G]](https://static.techno-science.net/illustration/Definitions/autres/a/ab29f0995b34cec76d165206dae54c3f_0490afbc7c4868465360c7e3f3ac0c02.png)
Ici si z est un complexe, z* désigne son conjugué.
Les caractères forment une base orthonormale de l'algèbre du groupe.
L'ensemble des caractères de
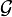
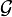
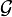
Les démonstrations sont données dans l'article détaillé.
Définition de la transformée de Fourier
Lorsque
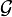
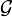
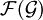

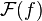
Cette application dispose de toutes les propriétés usuelles d'une transformée de Fourier, elle est linéaire, l'égalité de Parseval le théorème de Plancherel, la formule sommatoire de Poisson et la dualité de Pontryagin sont par exemple vérifiées. Il est aussi possible de définir un produit de convolution.
Les démonstrations sont données dans l'article détaillé.
Espace vectoriel fini
Il existe un cas important, celui où le groupe est un espace vectoriel fini V, donc de dimension fini sur un corps fini


Cet isomorphisme permet d'exprimer la transformation de Fourier d'un élément f de l'algèbre du groupe de V de la manière suivante :
Espace vectoriel sur le corps F2
Formes des caractères et isomorphisme avec le dual
On considère maintenant le cas où le corps

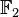
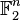
Il n'existe que deux caractères dans
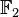
Transformation de Walsh
Dans le cas d'un espace vectoriel binaire (ie. sur le corps fini à deux éléments) la transformée de Fourier prend le nom de transformée de Walsh. Elle prend la forme suivante :
On remarque que le signe moins utilisé dans la définition disparait car dans
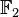
On voit donc que l'un des intérêts de cette identification est d'avoir la transformation de Walsh et son inverse qui agissent sur les mêmes objets : des fonctions de
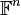
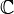
Formule de Poisson
Un autre intérêt de l'identification de
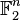
On remarque que
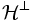
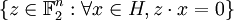
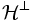
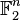
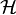
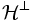
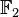
![\mathbb{F}[X_0,...,X_{n-1}]/(X_0^2+X_0,...,X_{n-1}^2+X_{n-1})](https://static.techno-science.net/illustration/Definitions/autres/0/0f675652bbb4e493f0e3a583ae9ec0d7_c6384929d6fd2793ecb09ab4468c2f00.png)
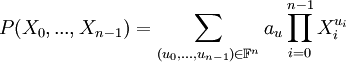
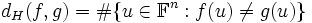
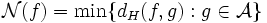
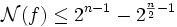
![\forall \chi_1, \chi_2 \in \mathbb C[\mathcal G] \quad <\chi_1 |\chi_2> = \frac 1{|\mathcal G|}\sum_{g \in \mathcal G} \chi_1(g)^*.\chi_2(g)](https://upload.wikimedia.org/math/d/7/d/d7df3d23d62316b63828808eb71cc705.png)