Algorithme de Knuth-Morris-Pratt - Définition

Introduction

L'algorithme de Knuth-Morris-Pratt (souvent abrégé par algorithme KMP) est un algorithme de recherche de sous-chaîne, permettant de trouver les occurrences d'une chaîne P dans un texte S. Sa particularité réside en un pré-traitement de la chaîne, qui fournit une information suffisante pour déterminer où continuer la recherche en cas de non-correspondance. Cela permet à l'algorithme de ne pas ré-examiner les caractères qui ont été précédemment vérifiés, et donc de limiter le nombre de comparaisons nécessaires.

L'algorithme a été inventé par Knuth et Pratt, et indépendamment par J. H. Morris en 1975.

Principe de fonctionnement

Approche naïve

Afin de mieux comprendre la logique de l'algorithme de Knuth-Morris-Pratt, il est instructif de se pencher sur l'approche naïve de la recherche de chaîne.

La chaîne P peut être trouvée dans le texte S avec l'algorithme suivant :

1. Fixer i = 1 ;
2. Tant qu'il reste des positions à vérifier
   • Comparer lettre à lettre la chaîne P et le texte S à partir de la position i ;
   • Si la chaîne correspond, terminer le traitement et retourner i comme position du début de l'occurrence ;
   • Sinon fixer i = i + 1 ;
3. Terminer le traitement, aucune occurrence n'a été trouvée.

Cette procédure peut être améliorée en arrêtant la comparaison de la deuxième étape dès qu'un caractère différent est détecté.

Cette approche a un inconvénient : après une comparaison infructueuse, la comparaison suivante débutera à la position i + 1, sans tenir aucun compte de celles qui ont déjà eu lieu à l'itération précédente, à la position i. L'algorithme de Knuth-Morris-Pratt examine d'abord la chaîne P et en déduit des informations permettant de ne pas comparer chaque caractère plus d'une fois.

Phases

1. La première phase de l'algorithme construit un tableau, indiquant pour chaque position un « décalage », c'est-à-dire la prochaine position où peut se trouver une occurrence potentielle de la chaîne.
2. La deuxième phase effectue la recherche à proprement parler, en comparant les caractères de la chaîne et ceux du texte. En cas de différence, il utilise le tableau pour connaître le décalage à prendre en compte pour continuer la recherche sans retour en arrière.

Exemple

Pour présenter le principe de fonctionnement de l'algorithme, un exemple particulier est considéré : la chaîne P vaut ABCDABD et le texte S est ABC ABCDAB ABCDABCDABDE.

Notations : Pour représenter les chaînes de caractères, cet article utilise des tableaux dont les indices débutent à zéro. Ainsi, le C de la chaîne P sera notée P[2]. m désigne la position dans le texte S à laquelle la chaîne P est en cours de vérification, et i la position du caractère actuellement vérifié dans P.

                    1         2          01234567890123456789012      m: v      S: ABC ABCDAB ABCDABCDABDE      P: ABCDABD      i: ^          0123456      

L'algorithme démarre en testant la correspondance des caractères les uns après les autres. Ainsi, à la quatrième étape, m = 0 et i = 3. S[3] est un espace et P[3] = 'D', la correspondance n'est pas possible.

                    1         2          01234567890123456789012      m: v      S: ABC ABCDAB ABCDABCDABDE      P: ABCDABD      i:    ^          0123456      

Plutôt que de recommencer avec m = 1, l'algorithme remarque qu'aucun A n'est présent dans P entre les positions 0 et 3, à l'exception de la position 0. En conséquence, pour avoir testé tous les caractères précédents, l'algorithme sait qu'il n'a aucune chance de trouver le début d'une correspondance s'il vérifie à nouveau. De ce fait, l'algorithme avance jusqu'au caractère suivant, en posant m = 4 et i = 0.

                    1         2          01234567890123456789012      m:     v      S: ABC ABCDAB ABCDABCDABDE      P:     ABCDABD      i:     ^              0123456      

Une correspondance presque complète est rapidement obtenue quand, avec i = 6, la vérification échoue.

                    1         2          01234567890123456789012      m:     v      S: ABC ABCDAB ABCDABCDABDE      P:     ABCDABD      i:           ^              0123456      

Toutefois, juste avant la fin de cette correspondance partielle, l'algorithme est passé sur le motif AB, qui pourrait correspondre au début d'une autre correspondance. Cette information doit donc être prise en compte. Comme l'algorithme sait déjà que ces deux premiers caractères correspondent avec les deux caractères précédant la position courante, il n'est pas nécessaire de les revérifier. Ainsi, l'algorithme reprend son traitement au caractère courant, avec m = 8 et i = 2.

                    1         2          01234567890123456789012      m:         v      S: ABC ABCDAB ABCDABCDABDE      P:         ABCDABD      i:           ^                  0123456      

Cette vérification échoue immédiatement (C ne correspond pas avec l'espace en S[10]). Comme la chaîne ne contient aucun espace (comme dans la première étape), l'algorithme poursuit la recherche avec m = 11 et en réinitialisant i = 0.

                    1         2          01234567890123456789012      m:            v      S: ABC ABCDAB ABCDABCDABDE      P:            ABCDABD      i:            ^                     0123456      

À nouveau, l'algorithme trouve une correspondance partielle ABCDAB, mais le caractère suivant C ne correspond pas au caractère final D de la chaîne.

                    1         2          01234567890123456789012      m:            v      S: ABC ABCDAB ABCDABCDABDE      P:            ABCDABD      i:                  ^                     0123456      

Avec le même raisonnement que précédemment, l'algorithme reprend avec m = 15, pour démarrer à la chaîne de deux caractères AB menant à la position courante, en fixant i = 2, nouvelle position courante.

                    1         2          01234567890123456789012      m:                v      S: ABC ABCDAB ABCDABCDABDE      P:                ABCDABD      i:                  ^                         0123456      

Cette fois, la correspondance est complète, l'algorithme retourne la position 15 (c'est-à-dire m) comme origine.

                    1         2          01234567890123456789012      m:                v      S: ABC ABCDAB ABCDABCDABDE      P:                ABCDABD      i:                      ^                         0123456      

L'algorithme de recherche

L'exemple précédent illustre de façon instructive le principe de l'algorithme. Il suppose l'existence d'un tableau donnant les « correspondances partielles » (décrit plus bas), indiquant où chercher le début potentiel de la prochaine occurrence, dans le cas où la vérification de l'occurrence potentielle actuelle échoue. Pour le moment, ce tableau, désigné par T, peut être considéré comme une boîte noire ayant la propriété suivante : si l'on dispose d'une correspondance partielle de S[m] à S[m + i − 1], mais qui échoue lors de la comparaison entre S[m + i] et P[i], alors la prochaine occurrence potentielle démarre à la position m + i − T[i − 1]. En particulier, T[ − 1] existe et est défini à − 1. Étant donné ce tableau, l'algorithme est relativement simple :

1. Fixer i = m = 0. Supposons que P a une longueur de n caractères, et S, de l caractères ;
2. Si m + i = l, alors terminer le traitement, aucune correspondance n'a été trouvée. Sinon, comparer P[i] et S[m + i] ;
   • S'ils sont égaux, fixer i = i + 1. Si i = n, alors la correspondance est complète. Terminer le traitement et retourner m comme position du début de la correspondance ;
   • S'ils sont différents, fixer e = T[i − 1]. Fixer m = m + i − e, et si i > 0, fixer i = e ;
3. Reprendre à l'étape n° 2.

Cette description met en œuvre l'algorithme appliqué dans l'exemple précédent. À chaque échec de la vérification, le tableau est consulté pour trouver le début de la prochaine occurrence potentielle, et les compteurs sont mis à jour en conséquence. De ce fait, la vérification des caractères n'est jamais effectuée vers l'arrière. En particulier, chaque caractère n'est vérifié qu'une seule fois (bien qu'il puisse être possiblement écarté plusieurs fois suite à l'échec de correspondances. Voir plus bas pour l'analyse de l'efficacité de l'algorithme).

Exemple de code de l'algorithme de recherche

Le morceau de code C qui suit est une implémentation de cet algorithme. Afin de pallier les limitations intrinsèques des tableaux en C, les indices sont décalés d'une unité, c'est-à-dire que T[i] dans le code est équivalent à T[i + 1] dans la description ci-dessus.

      int kmp_recherche(char *P, char *S)      {          extern int T[];          int m = 0;          int i = 0;                 // Tant que l'on a pas atteint la fin de la chaîne S ou de la chaîne P.          while (S[m + i] != '\0' && P[i] != '\0')          {              if (S[m + i] == P[i])              {                                    // Si on a encore une correspondance                  ++i;              // alors on regarde la lettre suivante              }              else              {                  // sinon                  m += i - T[i];    /* la prochaine correspondance partielle possible est à T[i]                                       lettre avant celle qu'on vient de regarder. */                         if (i > 0)                      i = T[i];     /* Puisque l'on sait que les T[i]-1 premières lettres à partir                                       de m sont bonne, il suffit de regarder P à partir de la T[i]ème                                       position. Pour S on peut remarquer que on m+i est maintenant                                       égale à (m+i-T[i])+(T[i]) avec les anciennes valeurs. Ce qui                                       montre qu'on ne retourne pas en arrière. */              }          }                 //Quand on a fini de parcourir une des deux chaines          if (P[i] == '\0')          {              //si la chaine finie est P alors on a trouvé une correspondance à la place m              return m;          }          else          {                    /* Sinon c'est qu'il n'existe pas de correspondance de                                  P dans S donc on renvoie un nombre impossible */              return m + i;    /* m est forcément le nombre de caractère de S, donc                                  m+1 est impossible. On pourrait aussi renvoyer -1 */          }      }      

Efficacité de l'algorithme de recherche

En supposant l'existence préalable du tableau T, la phase « recherche » de l'algorithme de Knuth-Morris-Pratt est de complexité O(l), où l désigne la longueur de S. Si l'on exclut les traitements supplémentaires fixes induits par l'entrée et la sortie de la fonction, tous les traitements sont effectués dans la boucle principale. Pour calculer une limite sur le nombre d'itérations, une première observation à propos de la nature de T est nécessaire. Par définition, il est construit de sorte que si une correspondance partielle débutant à S[m] échoue lors de la comparaison entre S[m + i] et P[i], alors la prochaine correspondance potentielle ne débute pas avant S[m + (i − T[i])]. En particulier, la prochaine correspondance potentielle doit se trouver à une position supérieure à m, de sorte que T[i] < i.

Partant de ce fait, on montre que la boucle s'exécute au plus l fois. À chaque itération, elle exécute une des deux branches de l'instruction if.

• La première branche augmente invariablement i et ne modifie pas m, ce qui fait que l'index m + i du caractère actuellement vérifié dans la chaîne S est augmenté.
• La seconde branche ajoute i − T[i] à m. Comme nous l'avons vu, i − T[i] est toujours positif. Ainsi, la position m du début de la correspondance potentielle actuelle est augmentée.

La boucle prend fin si , ce qui signifie, en tenant compte de la convention C spécifiant qu'un caractère NUL désigne la fin d'une chaîne, que m + i = l. En conséquence, chaque branche de l'instruction if peut être parcourue au plus l fois, puisqu'elles augmentent respectivement m + i ou m, et que , ainsi si m = l, alors , et comme l'augmentation à chaque itération est au minimum d'une unité, m + i = l a nécessairement été vérifié par le passé.

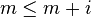
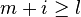
Ainsi, la boucle est exécutée au plus 2l fois, établissant par là-même une complexité algorithmique en O(l).