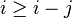Algorithme de Knuth-Morris-Pratt - Définition
La liste des auteurs de cet article est disponible ici.
Efficacité de l'algorithme de Knuth-Morris-Pratt
Comme les deux parties de l'algorithme ont respectivement des complexités de O(l) et O(n), la complexité de l'algorithme dans sa totalité est O(n + l).
Le tableau des « correspondances partielles »
L'objectif de ce tableau est de permettre à l'algorithme ne pas tester chaque caractère du texte plus d'une fois. L'observation-clé, à propos de la nature linéaire de la recherche, qui permet à cet algorithme de fonctionner, est qu'en ayant vérifié une partie du texte avec une « première portion » de la chaîne, il est possible de déterminer à quelles positions peuvent commencer les possibles occurrences qui suivent, et qui continuent de correspondre à la position courante dans le texte. En d'autres termes, les motifs (les sous-parties de la chaîne) sont « pré-recherchés » dans la chaîne, et une liste est établie, indiquant toutes les positions possibles auxquelles continuer pour sauter un maximum de caractères inutiles, sans toutefois sacrifier aucune occurrence potentielle.
Pour chaque position dans la chaîne, il faut déterminer la longueur du motif initial le plus long, qui se termine à la position courante, mais qui ne permet pas une correspondance complète (et qui vient donc très probablement d'échouer). Ainsi, T[i] désigne exactement la longueur du motif initial le plus long se terminant à P[i]. Par convention, la chaîne vide est de longueur nulle. Comme un échec au tout début de la chaîne est un cas particulier (la possibilité de backtracking n'existe pas), on pose T[ − 1] = − 1, tel que discuté précédemment.
En re-considérant l'exemple ABCDABD présenté précédemment, on peut établir qu'il fonctionne sur ce principe, et qu'il bénéficie de la même efficacité pour cette raison. On fixe T[ − 1] = − 1.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1
Comme P[0] n'apparaît qu'à la fin du motif initial complet, on fixe également T[0] = 0.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0
Pour déterminer T[1], l'algorithme doit trouver un motif terminal dans AB qui soit aussi un motif initial de la chaîne. Mais le seul motif terminal possible de AB est B, qui n'est pas un motif initial de la chaîne. De ce fait, T[1] = 0.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0 0
En poursuivant avec C, on remarque qu'il existe un raccourci pour vérifier tous les motifs terminaux. Considérons que l'algorithme ait trouvé un motif terminal de deux caractères de long, prenant fin sur le C ; alors le premier caractère de ce motif est un motif initial d'un motif initial de la chaîne, et par conséquent, un motif initial lui-même. De plus, il prend fin sur le B, pour lequel nous savons que la correspondance n'est pas possible. Ainsi, il n'est pas nécessaire de se soucier des motifs de deux caractères de longueur, et comme dans le cas précédent, l'unique motif de longueur unitaire ne correspond pas. Donc T[2] = 0.
De même pour D, on obtient T[3] = 0.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0 0 0 0
Pour le A suivant, le principe précédent nous montre que le motif le plus long à prendre en compte contient 1 caractère, et dans ce cas, A correspond. Ainsi, T[4] = 1.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0 0 0 0 1 P : A B C D A B D P : A B C D A B D
La même logique est appliquée sur B. Si l'algorithme avait trouvé un motif démarrant avant le A précédent, et se poursuivant avec le B actuellement considéré, alors il aurait lui-même un motif initial correct se terminant par A bien que débutant avant A, ce qui contredit le fait que l'algorithme a déjà trouvé que A est la première occurrence d'un motif s'y terminant. En conséquence, il n'est pas nécessaire de regarder avant le A pour y chercher un motif pour B. En fait, en le vérifiant, l'algorithme trouve qu'il continue par B et que B est la deuxième lettre du motif dont A est la première lettre. De ce fait, l'entrée pour B dans T est supérieur d'une unité à celle de A, c'est-à-dire T[5] = 2.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0 0 0 0 1 2 P : A B C D A B D P : A B C D A B D
Enfin, le motif ne continue pas de B vers D. Le raisonnement précédent montre que si un motif d'une longueur supérieure à 1 était trouvé sur D, alors il devrait contenir un motif se terminant sur B. Comme le motif courant ne correspond pas, il doit être plus court. Mais le motif courant est un motif initial de la chaîne se terminant à la deuxième position. Donc ce nouveau motif potentiel devrait lui aussi se terminer à la deuxième position, et nous avons déjà vu qu'il n'y en avait aucun. Comme D n'est pas lui-même un motif, T[6] = 0.
-1 0 1 2 3 4 5 6 i : v P[i]: A B C D A B D T[i]: -1 0 0 0 0 1 2 0
D'où le tableau suivant :
| i | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
| P[i] | A | B | C | D | A | B | D | |
| T[i] | -1 | 0 | 0 | 0 | 0 | 1 | 2 | 0 |
Algorithme de construction du tableau
L'exemple précédent illustre la technique générale pour produire le tableau avec le moins de soucis possible. Le principe est le même que pour la recherche générale : la majorité du traitement est déjà fait lors de l'arrivée sur un nouvelle position, il ne reste que peu de traitement pour passer à la suivante. Suit la description de l'algorithme. Pour éliminer des cas particuliers, la convention suivante est appliquée : P[ − 1] existe et sa valeur est différente de tous les caractères possibles de P.
- Fixer T[ − 1] = − 1. Supposons que P contienne n caractères ;
- Fixer i = 0 et j = − 1 ;
- Si i = n, terminer le traitement. Sinon, comparer P[i] et P[j].
- S'ils sont égaux, fixer T[i] = j + 1, j = j + 1 et i = i + 1 ;
- Sinon, et si j > 0, fixer j = T[j − 1] ;
- Sinon, fixer T[i] = 0, i = i + 1 et j = 0.
- Reprendre à l'étape n° 3.
Exemple de code de l'algorithme de construction du tableau
Le morceau de code C qui suit est une implémentation de cet algorithme. Comme pour l'algorithme de recherche, les indices de T ont été augmentés de 1 afin de rendre le code C plus naturel. La variable supplémentaire c permet de simuler l'existence de P[ − 1]. Il est supposé que cette fonction, ainsi que la fonction de recherche, sont appelées au sein d'une fonction de niveau supérieur, qui gère convenablement l'allocation de la mémoire pour le tableau T.
void kmp_tableau(char *P) { extern int T[]; int i = 0; int j = -1; char c = '\0'; //Donc c=P[-1] T[0] = j; //c'est-à-dire -1 while (P[i] != '\0') { //Tant que l'on a pas atteint la fin de la chaine /* ATTENTION la condition suivante est fausse, contre exemple avec la chaine "ABABABAB", il faut plutot mettre if((P[i] == P[j]) && j < ((i+(i%2))/2)) */ if (P[i] == c) { /* Si P[i]==P[j] donc si le caractère qu'on regarde est le même que le caractère suivant la fin * du dernier motif initial trouvé */ T[i + 1] = j + 1; //alors le motif est continué, et on incrémente i et j. ++j; ++i; } else if (j > 0) { //Sinon si au caractère précédant il existe un motif j = T[j]; //on va regarder le motif initial précédant qui peut correspondre a la lettre où l'on était. } else { /* Sinon j=0 ou -1, i.e. si les lettres qui précédent la ième suivie de la ième ne peuvent * correspondre a aucun marquage initiale */ T[i + 1] = 0; //alors on indique qu'il n'y a aucun motif initiale pour cette lettre. ++i; j = 0; //Cet affectation ne sert en fait que lorsque j=-1. } c = P[j]; } }
Cependant, remplacer int j=-1; par int j=0;, T[0] = j; par T[0] = -1; permettrait de supprimer l'affectation j = 0; sans rien changer au résultat de l'algorithme. On gagne un petit peu de temps d'exécution mais on perd de la cohérence parmi les variables.
Efficacité de l'algorithme de construction du tableau
La complexité de l'algorithme de construction du tableau est O(n), où n désigne la longueur de P. À l'exception des initialisations, tout le traitement est effectué dans l'étape n° 3. Ainsi, il suffit de montrer que cette étape s'exécute en O(n), ce qui est fait par la suite en examinant simultanément les quantités i et i − j.
- Dans la première branche, i − j est préservé, car i et j sont augmentés simultanément. La quantité i, elle, est donc augmentée.
- Dans la deuxième branche, j est remplacé par T[j − 1], qui est toujours strictement inférieur à j (voir plus haut), ce qui augmente i − j.
- Dans la troisième branche, i est augmenté, mais pas j, donc i et i − j sont tous deux augmentés.
Comme