Algorithme de colonies de fourmis - Définition

Introduction

Les algorithmes de colonies de fourmis sont des algorithmes inspirés du comportement des fourmis et qui constituent une famille de métaheuristiques d’optimisation.

Initialement proposé par Marco Dorigo et al. dans les années 1990, pour la recherche de chemins optimaux dans un graphe, le premier algorithme s’inspire du comportement des fourmis recherchant un chemin entre leur colonie et une source de nourriture. L’idée originale s'est depuis diversifiée pour résoudre une classe plus large de problèmes et plusieurs algorithmes ont vu le jour, s’inspirant de divers aspects du comportement des fourmis.

En anglais, le terme consacré à la principale classe d’algorithme est « Ant Colony Optimization » (abrégé ACO). Les spécialistes réservent ce terme à un type particulier d'algorithme. Il existe cependant plusieurs familles de méthodes s'inspirant du comportement des fourmis. En français, ces différentes approches sont regroupées sous les termes : algorithmes de colonies de fourmis, optimisation par colonies de fourmis, fourmis artificielles, ou diverses combinaisons de ces variantes.

Certains comportements des fourmis sont à l'origine d'algorithmes d’optimisation (ici, des fourmis légionnaires du genre Dorylus).

Origine

L’idée originale provient de l’observation de l’exploitation des ressources alimentaires chez les fourmis. En effet, celles-ci, bien qu’ayant individuellement des capacités cognitives limitées, sont capables collectivement de trouver le chemin le plus court entre une source de nourriture et leur nid.

1) la première fourmi trouve la source de nourriture (F), via un chemin quelconque (a), puis revient au nid (N) en laissant derrière elle une piste de phéromone (b). 2) les fourmis empruntent indifféremment les quatre chemins possibles, mais le renforcement de la piste rend plus attractif le chemin le plus court. 3) les fourmis empruntent le chemin le plus court, les portions longues des autres chemins perdent leur piste de phéromones.

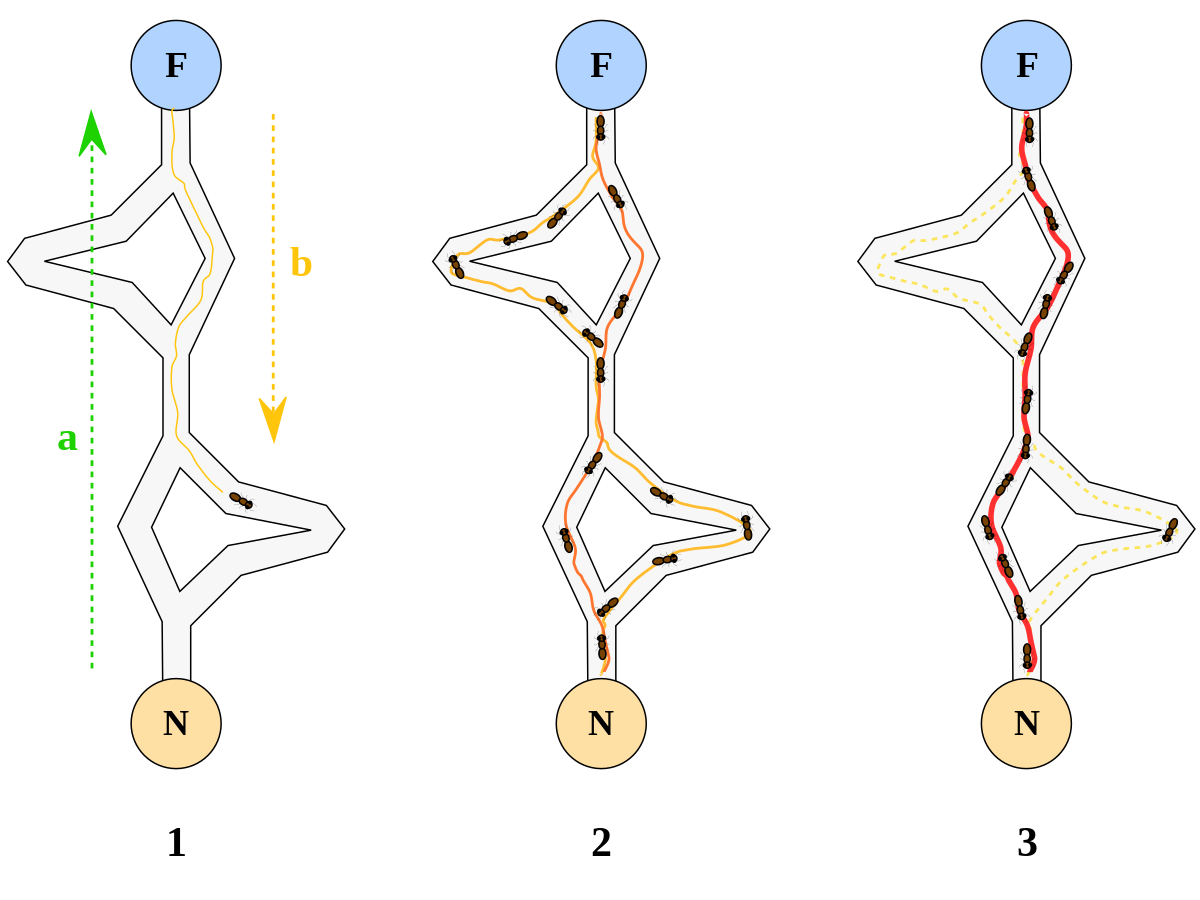
Des biologistes ont ainsi observé, dans une série d’expériences menées à partir de 1989, qu’une colonie de fourmis ayant le choix entre deux chemins d’inégale longueur menant à une source de nourriture avait tendance à utiliser le chemin le plus court.

Un modèle expliquant ce comportement est le suivant :

1. une fourmi (appelée « éclaireuse ») parcourt plus ou moins au hasard l’environnement autour de la colonie ;
2. si celle-ci découvre une source de nourriture, elle rentre plus ou moins directement au nid, en laissant sur son chemin une piste de phéromones ;
3. ces phéromones étant attractives, les fourmis passant à proximité vont avoir tendance à suivre, de façon plus ou moins directe, cette piste ;
4. en revenant au nid, ces mêmes fourmis vont renforcer la piste ;
5. si deux pistes sont possibles pour atteindre la même source de nourriture, celle étant la plus courte sera, dans le même temps, parcourue par plus de fourmis que la longue piste ;
6. la piste courte sera donc de plus en plus renforcée, et donc de plus en plus attractive ;
7. la longue piste, elle, finira par disparaître, les phéromones étant volatiles ;
8. à terme, l’ensemble des fourmis a donc déterminé et « choisi » la piste la plus courte.

Les fourmis utilisent l’environnement comme support de communication : elles échangent indirectement de l’information en déposant des phéromones, le tout décrivant l’état de leur « travail ». L’information échangée a une portée locale, seule une fourmi située à l’endroit où les phéromones ont été déposées y a accès. Ce système porte le nom de « stigmergie », et se retrouve chez plusieurs animaux sociaux (il a notamment été étudié dans le cas de la construction de piliers dans les nids de termites).

Le mécanisme permettant de résoudre un problème trop complexe pour être abordé par des fourmis seules est un bon exemple de système auto-organisé. Ce système repose sur des rétroactions positives (le dépôt de phéromone attire d’autres fourmis qui vont la renforcer à leur tour) et négatives (la dissipation de la piste par évaporation empêche le système de s'emballer). Théoriquement, si la quantité de phéromone restait identique au cours du temps sur toutes les branches, aucune piste ne serait choisie. Or, du fait des rétroactions, une faible variation sur une branche va être amplifiée et permettre alors le choix d’une branche. L'algorithme va permettre de passer d'un état instable où aucune branche n'est plus marquée qu'une autre, vers un état stable où l'itinéraire est formé des « meilleures » branches.