Algorithme de colonies de fourmis - Définition

Exemple : le « système fourmi »

Description générale

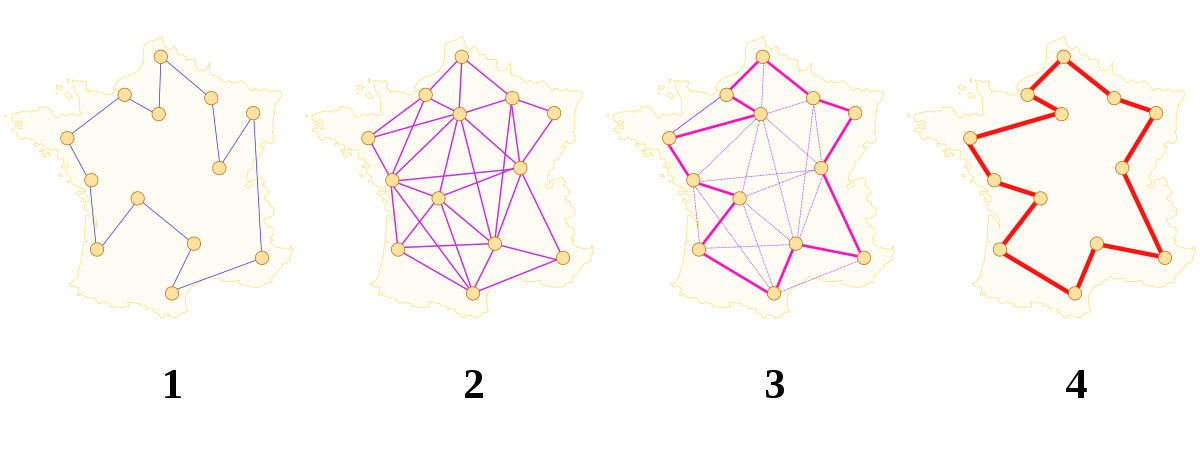
Le premier algorithme de colonies de fourmis proposé est appelé le Ant system (système fourmi). Il vise notamment à résoudre le problème du voyageur de commerce, où le but est de trouver le plus court chemin permettant de relier un ensemble de villes.

L’algorithme général est relativement simple, et repose sur un ensemble de fourmis, chacune parcourant un trajet parmi ceux possibles. À chaque étape, la fourmi choisit de passer d’une ville à une autre en fonction de quelques règles :

1. elle ne peut visiter qu’une fois chaque ville ;
2. plus une ville est loin, moins elle a de chance d’être choisie (c’est la « visibilité ») ;
3. plus l'intensité de la piste de phéromone disposée sur l’arête entre deux villes est grande, plus le trajet aura de chance d’être choisi ;
4. une fois son trajet terminé, la fourmi dépose, sur l’ensemble des arêtes parcourues, plus de phéromones si le trajet est court ;
5. les pistes de phéromones s’évaporent à chaque itération.

L’algorithme « Ant System » optimisant le problème du voyageur de commerce : 1) une fourmi choisit un trajet, et trace une piste de phéromone. 2) l’ensemble des fourmis parcourt un certain nombre de trajets, chaque fourmi déposant une quantité de phéromone proportionnelle à la qualité du parcours. 3) chaque arête du meilleur chemin est plus renforcée que les autres. 4) l’évaporation fait disparaître les mauvaises solutions.

Description formelle

La règle de déplacement est appelée « règle aléatoire de transition proportionnelle », et est écrite mathématiquement sous la forme suivante :

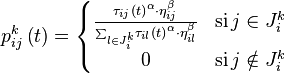
Où J_i^k est la liste des déplacements possibles pour une fourmi k lorsqu’elle se trouve sur une ville i, η_ij la visibilité, qui est égale à l’inverse de la distance de deux villes i et j (1/d_ij) et τ_ij (t) l’intensité de la piste à une itération donnée t. Les deux principaux paramètres contrôlant l’algorithme sont α et β, qui contrôlent l’importance relative de l’intensité et de la visibilité d’une arête.

Une fois la tournée des villes effectuée, une fourmi k dépose une quantité de phéromone sur chaque arête de son parcours :

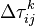
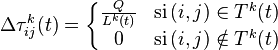
Où T^k (t) est la tournée faite par la fourmi k à l’itération t, L^k (t) la longueur du trajet et Q un paramètre de réglage.

À la fin de chaque itération de l’algorithme, les phéromones déposées aux itérations précédentes par les fourmis s’évaporent de :

ρτ_ij(t)

Et à la fin de l'itération, on a la somme des phéromones qui ne se sont pas évaporées et de celles qui viennent d'être déposées.

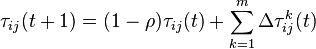
Où m est le nombre de fourmis utilisées pour l’itération t et ρ un paramètre de réglage.

Historique

• 1959, Pierre-Paul Grassé invente la théorie de la stigmergie pour expliquer le comportement de construction du nid chez des termites ;
• 1983, Deneubourg et ses collègues étudient le comportement collectif des fourmis ;
• 1988, Moyson et Manderick présentent un article sur l’auto-organisation chez les fourmis ;
• 1989, travaux de Goss, Aron, Deneubourg et Pasteels, sur le comportement collectifs des fourmis Argentines, qui donneront l’idée des algorithmes de colonies de fourmis ;
• 1989, implémentation d’un modèle de comportement de recherche de nourriture par Ebling et ses collègues ;
• 1991, M. Dorigo propose le Ant System dans sa thèse de doctorat (qui ne sera publiée qu’en 1992). Il fait paraître, avec V. Maniezzo et A. Colorni, un rapport technique, qui sera publié cinq ans plus tard ;
• 1995, Bilchev et Parmee publient la première tentative d'adaptation aux problèmes continus ;
• 1996, publication de l'article sur le Ant System ;
• 1996, Stützle et Hoos inventent le MAX-MIN Ant Sytem ;
• 1997, Dorigo et Gambardella publient le Ant Colony System ;
• 1997, Schoonderwoerd et ses collègues conçoivent la première application aux réseaux de télécommunications ;
• 1997, Martinoli et ses collègues s’inspirent des algorithmes de colonies de fourmis pour le contrôle de robots ;
• 1998, Dorigo lance la première conférence dédiée aux algorithmes de colonies de fourmis ;
• 1998, Stützle propose les premières implémentations parallèles ;
• 1999, Bonabeau et ses collègues font paraître un livre traitant principalement des fourmis artificielles ;
• 1999, premières applications pour le routage de véhicule, l’assignement quadratique, le sac à dos multi-dimensionnel ;
• 2000, numéro spécial d’une revue scientifique sur les algorithmes de colonies de fourmis ;
• 2000, premières applications à l’ordonnancement, l’ordonnancement séquentiel, la satisfaction de contraintes ;
• 2000, Gutjahr donne la première preuve de convergence pour un algorithme de colonies de fourmis ;
• 2001, première utilisation des algorithmes de colonies de fourmis par des entreprises (Eurobios et AntOptima) ;
• 2001, Iredi et ses collègues publient le premier algorithme multi-objectif ;
• 2002, premières applications à la conception d’emploi du temps, les réseaux bayésiens ;
• 2002, Bianchi et ses collègues proposent le premier algorithme pour problème stochastique ;
• 2004, Zlochin et Dorigo montrent que certains algorithmes sont équivalents à la descente stochastique de gradient, l'entropie croisée et les algorithmes à estimation de distribution ;
• 2005, premières applications au repliement de protéines.