Anneau non commutatif de polynômes - Définition
La liste des auteurs de cet article est disponible ici.
Définition de la structure d'algèbre sur un anneau commutatif A
Si A est commutatif, la multiplication
![A\times A[X]\to A[X]](https://static.techno-science.net/illustration/Definitions/autres/5/5ae5408a6daad815f1c4bb35d2190bdd_9c66f7cdf1778a67b02a0e10819ba527.png)
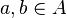
![P,Q\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/0/0ad493123a377bb3d919c579ad1e18f7_41eb86b74b34c68ef40cc17beeae2b1a.png)
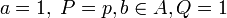
Divisions par X − u
Comme le coefficient dominant 1 du polynome X − u est évidemment inversible, les divisions à droite et à gauche sont possibles. Soient
![P \in A[X]](https://static.techno-science.net/illustration/Definitions/autres/9/98f3ed572879618603c8413eab5ee1cb_35aec4043775e480a28d61fafd7048b5.png)
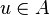
Le reste de la division à gauche du polynôme P par X − u est égal à la valeur à droite Pd(u).
Posons
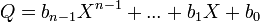
On a P = Q(X − u) + R et en groupant les termes de même degré du second membre :
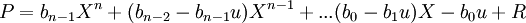
Si on remplace alors X par u dans le membre de droite (ce qui est bien le calcul de la valeur à droite) on constate immédiatement que les termes provenant du produit Q(X − u) s'annulent 2 à 2 et on obtient le résultat annoncé.
Remarquons que, lorsque u n'est pas central, on ne pouvait pas faire appel au théorème précédent et raisonner que Pd(u) = Qd(u)(X − u)d(u) + R = Qd(u).0 + R = R. Mais en reprenant la preuve de ce théorème on peut justifier néanmoins cette formule. On observe que dans cette preuve on a écrit P[X: = u] sous la forme de la valeur à droite, et que la preuve n'a utilisé que la commutation de u avec les coefficients bj du polynome à droite ; or, dans la formule considérée cette commutation est valable car les seuls coefficients du polynome X − u à droite sont b1 = 1 et b0 = u, qui commutent avec u.
On a le résultat symétrique :
- Le reste de la division à droite du polynôme P par X − u est égal à la valeur à gauche Pg(u).
Le polynôme P est divisible à gauche par X − u si et seulement si Pd(u) = 0 et le polynôme P est divisible à droite par X − u si et seulement si Pg(u) = 0

















































