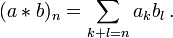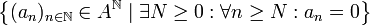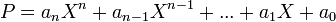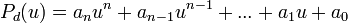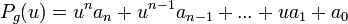Anneau non commutatif de polynômes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le but de cet article est de montrer comment on obtient l'anneau des polynômes à une variable (ou indéterminée) sur un anneau unitaire non nécessairement commutatif.
Le cas des anneaux de polynômes sur un anneau commutatif unifère est traité dans les articles Construction de l'anneau des polynômes et Polynôme formel (à une indéterminée) et dans l'article Polynôme en plusieurs indéterminées. Dans ce dernier, un autre type d'anneau non commutatif de polynômes est construit : l'algèbre d'un monoïde.
Préliminaires
On se donne un anneau unitaire A.
On va construire :
- l'ensemble A[X] ;
- une structure d'anneau unitaire sur cet ensemble, commutatif si A l'est, et intègre si A l'est ;
- une structure de A-algèbre sur cet ensemble, si A est commutatif.
On va prouver
- l'existence d'une opération de division euclidienne, ou deux telles opérations à droite et à gauche si A est non-commutatif, par tout polynôme à coefficient dominant inversible dans A, avec quotient et reste uniques,
- et son rapport avec l'évaluation (à droite ou à gauche) des polynômes en un élément de A.
Définition de la structure d'anneau
Commençons par définir ce mystérieux X, appelé indéterminée : il s'agit de la suite nulle partout, sauf à l'indice 1 où elle vaut 1. On note par ailleurs que l'on peut envoyer A dans A[X] de façon injective par l'application qui à un élément a associe la suite dont le coefficient à l'indice 0 vaut a, et qui est nulle partout ailleurs.
Pour définir la structure de groupe additif sur A[X], on se contente de reprendre la structure héritée naturellement par le fait que ce sont des suites à valeurs dans un anneau : la suite a + b est donnée par (a + b)n = (a)n + (b)n. L'élément neutre est la suite entièrement nulle. La structure multiplicative est un peu plus compliquée : la suite a * b est donnée par
Comme les suites a et b n'ont qu'un nombre fini de coefficients non nuls, il en est de même pour a + b et a * b. La formule pour a * b définit bien une loi de composition interne associative et commutative, dont l'image de l'élément 1 de A par l'application injective
![A\to A[X]](https://static.techno-science.net/illustration/Definitions/autres/2/2bd54127c060c8729b3d0cb5ec341c9a_5c2a1ca88f36f08db54bd738ccbe85a9.png)
Et avec cette addition et cette multiplication, il est clair que l'on a bien une structure d'anneau. Il reste à remarquer que Xn est la suite nulle partout sauf en n, où elle vaut 1 ; en particulier, tout polynôme P = (an)n s'écrit donc de façon unique : :
| P = | ∑ | anXn |
| n |
On retrouve là l'écriture habituelle des polynômes.
Définition de l'ensemble
On va considérer les suites d'éléments de A, nulles à partir d'un certain rang. Cet ensemble peut-être vu comme la partie de l'ensemble
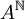
C'est notre ensemble A[X].
Division euclidienne à droite (resp. à gauche)
On se donne deux polynômes P et U. On ne fait pas d'hypothèse sur le premier, mais on demande que le coefficient dominant du second soit inversible.
On souhaite prouver qu'il existe un unique couple de polynômes Q et R réunissant les deux conditions suivantes :
-
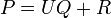
-
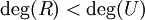
Q sera le quotient et R le reste dans la division à droite. On dira aussi que Q est le quotient à droite et R le reste à droite.
Si R=0 on dira naturellement que P est divisible à droite par U.
De manière symétrique on désignera par quotient à gauche et reste à gauche les polynômes Q' et R' vérifiant :
-
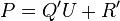
-
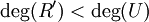
et si R=0, P sera dit divisible à gauche par U.
Il est évident que ces 2 notions coïncident dans le cas d'un anneau commutatif. Nous ferons la démonstration de l'unicité et de l'existence du quotient et du reste dans le premier cas seulement, l'adaptation au second cas ne posant aucune difficulté.
Unicité
Supposons que l'on a deux couples (Q1,R1) et (Q2,R2) qui vérifient les conditions requises ; on a alors, en calculant P − P : U(Q1 − Q2) = R2 − R1.
Mais si on compare les degrés des polynômes dans les membre gauche et droit de cette égalité, on doit alors clairement avoir: R1 = R2 et U(Q1 − Q2) = 0. Donc on a déjà l'unicité du reste.
Le fait que U est non nul ne suffit pas à conclure que Q1 = Q2, car A[X] n'est intègre que si A l'est (ce qu'on n'a pas supposé). En revanche, on sait que le coefficient dominant de U est inversible, et c'est cette remarque qui permet de conclure à l'unicité du quotient.
Existence
On la montre par récurrence sur le degré du polynôme P :
- si ce degré est plus petit que le degré de U, il suffit de prendre Q = 0 et R = P ;
- s'il est supérieur ou égal, notons a le coefficient dominant de P, et b celui de U; alors si on regarde le polynôme P − ab − 1UXdegP − degU, on voit qu'il est de degré strictement inférieur à celui de P, donc par hypothèse de récurrence, il s'écrit Q2U + R2 ; mais alors
- P = (Q2 + ab − 1XdegP − degU)U + R2
Remarques
- Pour l'unicité, on aurait pu supposer que le coefficient dominant de U n'était que régulier ; en revanche pour l'existence, cette inversibilité est nécessaire (voir l'article Division d'un polynôme).
- L'unicité est traitée en premier, car sans le dire, c'est elle qui pointe vers l'existence, en utilisant la notion de degré d'un polynôme.
Valeur à droite (resp. à gauche) d'un polynôme pour un élément de l'anneau
Soient
![P\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/9/98f3ed572879618603c8413eab5ee1cb_35aec4043775e480a28d61fafd7048b5.png)
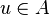
Nous désignons par valeur à droite de P pour X = u l'élément de A :
De même la valeur à gauche sera :
Théorème Si u est un élément central de A (et donc pour tout
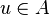
![P\in A[X]](https://static.techno-science.net/illustration/Definitions/autres/9/98f3ed572879618603c8413eab5ee1cb_35aec4043775e480a28d61fafd7048b5.png)
![P\mapsto P[X:=u]](https://static.techno-science.net/illustration/Definitions/autres/c/cc80d22562500b7f3aa066e8176d5db3_798fdad1949922a3e0853fb29ee6eeb7.png)
![A[X]\to A](https://static.techno-science.net/illustration/Definitions/autres/9/97ad3d15eb1842cef511f63aaec0ba25_f1396de5e027f327bf9652028ae32d55.png)
Preuve. Comme u commute avec tous les coefficients de P, les valeurs à gauche et à droite sont égales. Que
![P\mapsto P[X:=u]](https://static.techno-science.net/illustration/Definitions/autres/c/cc80d22562500b7f3aa066e8176d5db3_798fdad1949922a3e0853fb29ee6eeb7.png)
| P = | ∑ | aiXi |
| i |
et
| Q = | ∑ | bjXj |
| j |
alors on a
| P[X: = u]Q[X: = u] = | ∑ | aiuibjuj = | ∑ | aibjui + j = PQ[X: = u] |
| i,j | i,j |
grâce à la commutation de ui avec les coefficients bj.