Apollonios de Perga - Définition

L'analyse des Anciens

Outre les Coniques, Pappus mentionne plusieurs autres traités d'Apollonius (les titres en latin sont dus à Commandino) :

1. Λόγου ἀποτομή, De Rationis Sectione (« Sur la section de rapport »)
2. Χωρίου ἀποτομή, De Spatii Sectione (« Sur la section d'aire »)
3. Διωρισμένη τομή, De Sectione Determinata (« Sur la Section déterminée »)
4. Ἐπαφαί, De Tactionibus (« Les Contacts »)
5. Νεύσεις, De Inclinationibus (« Les inclinaisons »)
6. Τόποι ἐπίπεδοι, De Locis Planis (« Les lieux plans »)

Ces traités, dont chacun comprenait deux livres, étaient compilés à l'époque où vivait Pappus avec les Coniques et trois ouvrages d'Euclide (le Livre des données, les Porismes et les Lieux plans) sous le titre générique de « Trésor de l'Analyse ».

Le propos de l'Analyse des Anciens, tel que l'expose Pappus dans le livre VII de sa « Collection Mathématique », était de trouver une construction à la règle et au compas d'un lieu géométrique donné, ou du moins d'inventorier les cas où une telle construction était possible. Malheureusement, Pappus n'a transmis que des résumés des livres d'Apollonius, de sorte que l'étendue et la portée des méthodes de l'analyse a fait l'objet de multiples gloses du XVI^e au XVIII^e siècle. S'appuyant sur les indices donnés par Pappus et leurs spéculations personnelles, une pléiade de mathématiciens fameux se sont essayés à reconstruire les traités perdus d'Apollonius dans leur ordre original.

La Section de rapport

Les deux livres du traité De rationis sectione sont consacrés au problème suivant : étant données deux droites et un point sur chacune d'elle, mener depuis un troisième point une droite telle qu'elle découpe deux segments (entre chaque point donné et le point d'intersection) dont les longueurs soient dans un rapport donné.

La Section d'aire

Les deux livres du traité De Spatii Sectione discutent la résolution d'un problème similaire au précédent : il s'agit cette fois de découper deux segments dont le produit soit égal à un produit donné ; dans la terminologie géométrique des Anciens, l'énoncé demande que les deux segments déterminent un rectangle de surface égale à un rectangle donné.

Une copie arabe de « La Section de rapport » fut retrouvée à la fin du XVII^e siècle par Edward Bernard à la Bodleian Library. Bien qu'il eût commencé la traduction de ce document, ce fut Halley qui la mena à terme, et qui la publia en 1706 avec sa reconstitution du De Spatii Sectione.

La Section déterminée

Le traité traduit par Commandino sous le titre De Sectione Determinata traite pour ainsi dire de problèmes à une dimension d'espace : il s'agit ici de construire sur une droite des segments qui soient dans un rapport donné. Plus précisément, les problèmes abordés sont les suivants : étant donnés deux, trois ou quatre points sur une droite, trouver un point tel que les segments qu'il forme avec les autres points déterminent deux à deux des rectangles qui soient dans un rapport donné ; ainsi :

• si deux points A, B sont donnés, trouver M tel que soit égal à un rapport k donné ;
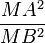
• si trois points A, B, C sont donnés, trouver M tel que soit égal à un rapport k donné. Une variante étudiée par Apollonius consiste à donner, outre A, B, C, un segment PQ et à chercher le(s) point(s) M tel que
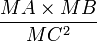
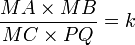
• si quatre points A, B, C, D sont donnés, trouver M tel que soit égal à un rapport k donné.

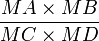
Parmi les mathématiciens qui ont cherché à retrouver la solution d'Apollonius, citons :

• Snellius (Apollonius Batavus, Leyde, 1608);
• Alexander Anderson d'Aberdeen, dans son supplément à Apollonius Redivivus (Paris, 1612);
• et Robert Simson dans ses Opera quaedam reliqua (Glasgow, 1776), de loin la reconstitution la plus détaillée et la plus convaincante.

Les Contacts

Le traité De Tactionibus est consacré au problème générique suivant : trois éléments (points, droites ou cercles ; éventuellement un point, une droite et un cercle ; ou deux droites et un cercle, etc.) étant donnés de position, décrire un cercle passant par ces points, ou tangent à ces droites ou à ces cercles.

Le cas le plus difficile et le plus intéressant historiquement parlant est celui où les trois données sont trois cercles. François Viète, à la fin du XVI^e siècle, proposa ce problème (dit Problème d'Apollonius) à Adrien Romain, qui ne put le résoudre qu'en utilisant une hyperbole auxiliaire pour la construction. Viète lui répondit en publiant une solution « à la règle et au compas » (c'est-à-dire conforme aux exigences de l'analyse des Anciens), dans son livre Apollonius Gallus (Paris, 1600).

Les Inclinaisons

Le propos du livre intitulé De Inclinationibus consiste à insérer un segment de longueur donnée entre deux droites sécantes (ou deux cercles, ou une droite et un cercle), de telle façon que ce segment, prolongé, passe par un point donné. Marin Ghetaldi et Hugo d'Omerique (Analyse géometrique, Cadix, 1698) se sont essayés à ce problème, mais la reconstitution la plus satisfaisante est sans doute celle de Samuel Horsley (1770).

Les Lieux plans

De Locis Planis contient un ensemble de propositions relatives à des lieux qui s'avèrent être des droites ou des cercles. Comme Pappus ne donne que des cas particuliers de ce type de problème, les géomètres modernes ont longtemps été réduits aux conjectures pour trouver l'idée directrice de cette catégorie d'énoncés. Aussi chacun y est-il allé de son interprétation, à commencer par Pierre de Fermat (1636, publiée finalement dans ses Œuvres, tome I, 1891, pp. 3-51). Suivirent entre autres Frans van Schooten (Leyde, 1656) et Robert Simson (Glasgow, 1749).