Axiome du choix - Définition
La liste des auteurs de cet article est disponible ici.
Anecdote
Bertrand Russell disait à propos de l'axiome du choix : Pour choisir une chaussette plutôt que l'autre pour chaque paire d'une collection infinie, on a besoin de l'axiome du choix. Mais pour les chaussures, ce n'est pas la peine.
Explication :
- Quand on dispose d'une paire de chaussettes quelconque, on n'a aucun moyen a priori de distinguer une chaussette de l'autre, ce sont des objets a priori identiques et même si chaque matin on arrive à choisir laquelle on va mettre en premier, on serait bien en peine de trouver un procédé général qui nous permette de renouveler l'exploit éternellement.
- Pour les chaussures, il existe un moyen de choisir qui marche tout le temps (une fonction de choix naturelle) : choisir toujours la chaussure gauche (ou droite) puisqu'il y a toujours une chaussure gauche et une chaussure droite.
On pourrait penser que c'est une interprétation forcée de l'axiome. Mais Paul Cohen a montré en 1962 qu'il était possible de construire un modèle de ZF dans lequel une certaine réunion dénombrable d'ensembles à deux éléments n'est pas dénombrable, confirmant l'intuition de Russell.
Formes faibles de l'axiome du choix
Il existe des formes faibles de l'axiome du choix que le mathématicien utilise couramment, la plupart du temps sans s'en apercevoir à moins d'être logicien ou « constructiviste », et qui servent à « construire » des suites. Elles sont absolument indispensables pour l'exposé usuel des fondements de l'analyse.
Axiome du choix dénombrable
Cet axiome, abrégé en « AD », est la restriction de l'axiome du choix aux familles dénombrables :
-
- « Étant donnée une famille dénombrable d'ensembles non vides, il existe une fonction qui à chacun d'entre eux associe un de ses éléments. »
Il est par exemple utilisé pour démontrer qu'une fonction f définie sur R est continue en 0 ssi f(xn) tend vers f(0) pour toute suite (xn) tendant vers 0. Il permet aussi de démontrer qu'un produit dénombrable d'espaces compacts est compact, ou encore le théorème de Hahn-Banach pour un espace de Banach séparable. Il permet également de démontrer le théorème des complets emboîtés (dont l'une des conséquences est le théorème de Baire).
Attention à une confusion courante : c'est la famille d'ensembles qui est dénombrable, aucune hypothèse n'étant faite sur les ensembles composant cette famille. L'axiome du choix dénombrable ne concerne pas la question du choix d'un élément dans un ensemble dénombrable mais la possibilité de faire une infinité dénombrable de choix simultanément.
Axiome du choix dépendant
Cet axiome, abrégé en « DC », assure que, si R est une relation sur un ensemble non vide E vérifiant
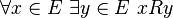
alors il existe une suite (xn) d'éléments de E telle que