Ensemble dénombrable - Définition

Introduction

En mathématiques, un ensemble est dit dénombrable, ou infini dénombrable, lorsque ses éléments peuvent être listés sans omission ni répétition dans une suite indexée par les entiers. Certains ensembles infinis, au contraire, contiennent « trop » d'éléments pour être parcourus complètement par l'infinité des entiers et sont donc dits « non dénombrables ».
On comprend parfois parmi les ensembles dénombrables les ensembles finis, dont les éléments peuvent être numérotés par les entiers positifs inférieurs à une valeur donnée. Cependant, il est devenu assez courant de réserver l'adjectif « dénombrable » aux seuls ensembles infinis.

Georg Cantor est le premier à faire usage de cette notion, dans un article publié en 1874, qui marque la naissance de la théorie des ensembles. Mais l'importance du dénombrable se manifeste dans de nombreux domaines des mathématiques, notamment en analyse, en théorie de la mesure et en topologie.

Définitions

Plus formellement un ensemble E est dit dénombrable quand il est équipotent à l'ensemble des entiers naturels N, c'est-à-dire qu'il existe une bijection de N sur E. Cette définition est parfois élargie aux ensembles finis par certains auteurs, qui définissent un ensemble dénombrable comme un ensemble en bijection avec un sous-ensemble des entiers naturels. Mais cet élargissement sera désigné dans cet article par l'expression « ensemble au plus dénombrable » ou encore « ensemble fini ou dénombrable ».. S'il y a risque d'ambiguïté, un ensemble équipotent à N peut toujours être précisé « ensemble infini dénombrable ».

A contrario, un ensemble (infini) non dénombrable, est un ensemble infini qui n'est pas équipotent à N. L'argument de la diagonale de Cantor permet de montrer que l'ensemble des réels et l'ensemble des parties de N ne sont pas dénombrables, mais aussi l'existence de « nombreux » autres infinis non dénombrables.

Un ensemble qui contient un ensemble infini dénombrable est nécessairement infini, c'est-à-dire qu'il n'est équipotent à aucun ensemble borné d'entiers naturels. Dès que l'on se donne suffisamment d'axiomes en théorie des ensembles, en particulier l'axiome du choix, on montre que l'infini dénombrable est le plus petit infini, au sens où tout ensemble infini contient un ensemble infini dénombrable. La réciproque ne pose pas de difficulté. On peut alors caractériser un ensemble infini comme un ensemble contenant un ensemble dénombrable.

Le cardinal de N, et donc le cardinal de n'importe quel ensemble dénombrable, est noté ℵ₀ (aleph zero). Il est le premier de la suite ordinale des alephs, qui représentent tous les cardinaux infinis en présence de l'axiome du choix.

Quelques exemples d'ensembles dénombrables

Sous-ensembles de N

L'ensemble N des entiers naturels est bien sûr dénombrable par définition, mais, comme cela sera démontré ultérieurement, chacun de ses sous-ensembles infinis l'est également. On peut expliciter quelques cas particuliers. la remarque que N pouvait être mis en correspondance avec une partie stricte a été faite à plusieurs reprises dès l'antiquité. On cite par exemple souvent Galilée pour la remarque qu'il y a « autant » de carrés parfaits que d'entiers naturels. De la même façon, on obtient par une énumération explicite :

• l'ensemble N^∗ des entiers naturels non nuls est dénombrable, il est énuméré par la suite (n+1) ;
• l'ensemble des entiers naturels pairs est dénombrable, car énuméré par la suite (2n).

Dans le cas des nombres premiers on peut utiliser une définition par récurrence :

• l'ensemble des nombres premiers est dénombrable ; on définit par récurrence une suite (p_n) qui énumère les nombres premiers en posant :

p₀=2 ;

p_n+1 est le plus petit nombre premier strictement supérieur à p_n.

La démonstration d'Euclide, qui montre que l'ensemble des nombres premiers est infini, permet d'assurer également que p_n+1 est bien défini, puisque l'ensemble des nombres premiers strictement supérieurs à p_n est forcément non vide (en l'occurrence il contient le ou les diviseurs premiers de p₀.p₁ … p_n+1).

La méthode utilisée dans ce dernier cas est suffisamment générale pour s'adapter à tout sous-ensemble infini des entiers naturels.

« Sur-ensembles » de N

On montre que certains ensembles qui ont N, ou une copie évidente de N, pour partie stricte, sont dénombrables.

Les entiers relatifs.

L'ensemble Z des entiers relatifs est dénombrable. En effet, la suite ((-1)ⁿ⌈n/2⌉), où ⌈n/2⌉ désigne le plus petit nombre entier supérieur ou égal à n/2, établit bien une bijection des entiers naturels dans les entiers relatifs : les termes d'indices pairs décrivent les entiers naturels, ceux d'indice impair les entiers négatifs non nuls.

Les couples d'entiers naturels

La fonction de couplage de Cantor établit une bijection de N × N dans N.

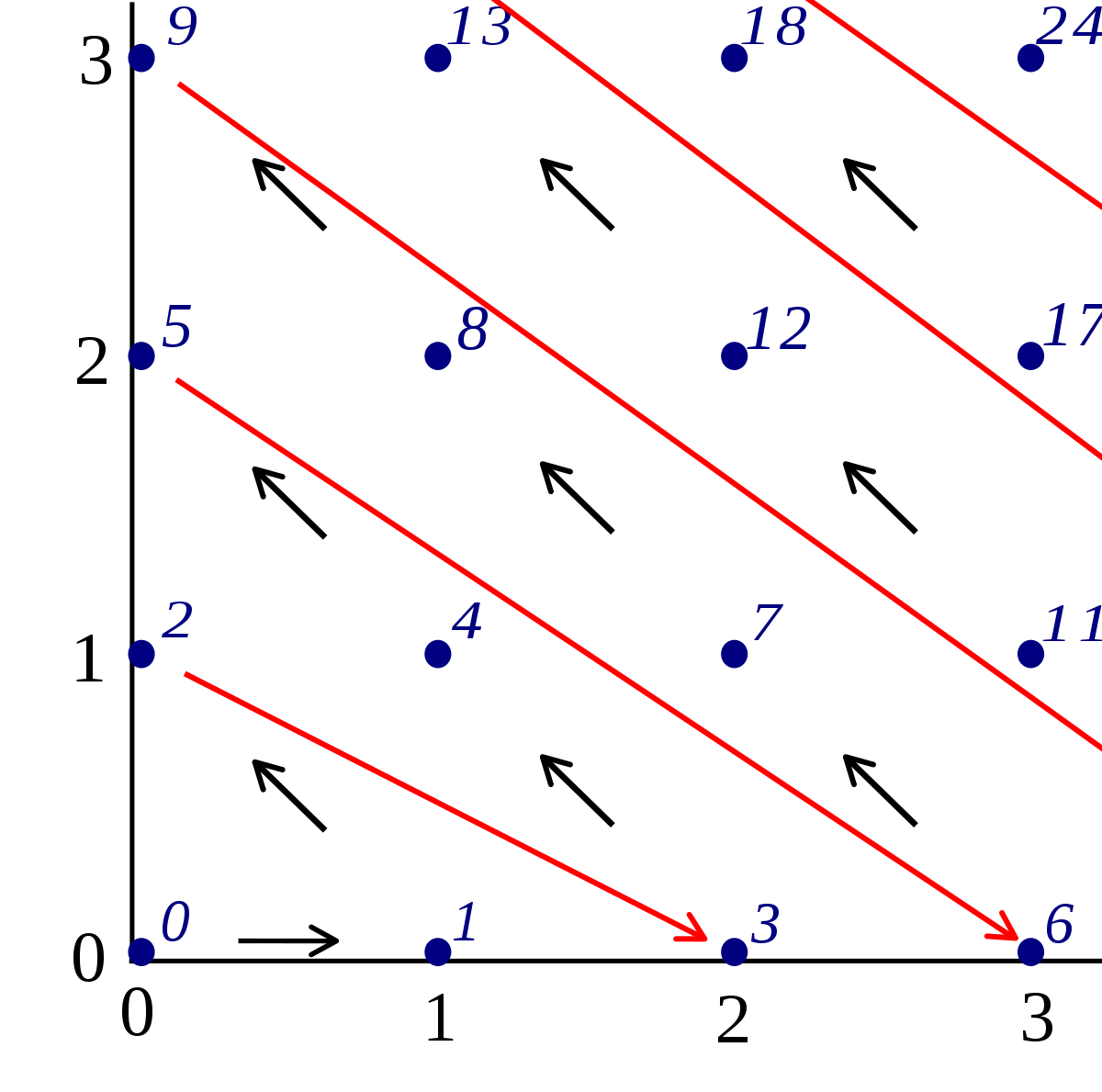
L'ensemble N × N des couples d'entiers naturels est dénombrable, on peut énumérer les couples d'entiers naturels diagonale par diagonale, comme indiqué sur le schéma joint : en le suivant on définit facilement par récurrence une suite de couples qui énumère bijectivement tous les couples d'entiers naturels. La réciproque de cette fonction, soit f, qui est donc une bijection de N × N dans N, dite fonction de couplage est un polynôme de degré 2 :

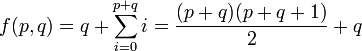
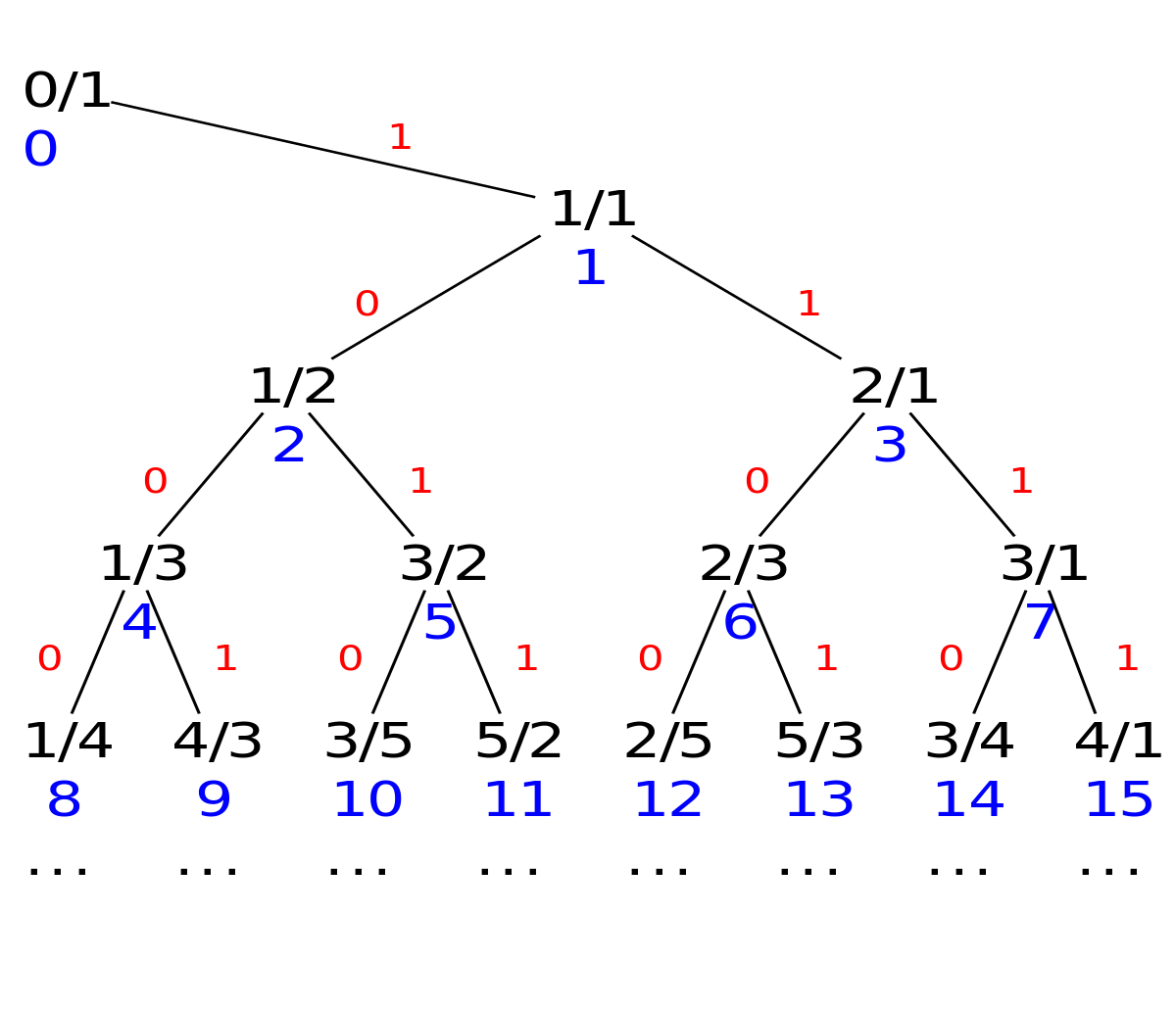
Les rationnels

Une variante due à Neil Calkin et Herbert Wilf de l'arbre de Stern-Brocot donne une bijection simple à calculer des rationnels positifs ou nuls, plus précisément de leurs représentations par des fractions irréductibles, dans les entiers naturels : la fraction irréductible a/b a pour fils gauche a/(a+b) et pour fils droit (a+b)/b ; ces fractions sont irréductibles. Toute fraction irréductible d'entiers apparait une et une seule fois dans l'arbre (voir l'algorithme d'Euclide par soustraction original). Le chemin de la racine 0/1 au noeud a/b donne la représentation binaire de l'entier image de a/b par la bijection. La bijection réciproque peut se définir par récurrence :
    
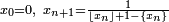
où ⌊x_n⌋ est la partie entière de x_n et x_n=⌊x_n⌋ + {x_n}.

L'ensemble Q des nombres rationnels est dénombrable. En effet un rationnel est représenté par une fraction, c'est-à-dire un couple constitué d'un entier relatif et d'un entier naturel non nul. En composant comme il faut les bijections établies précédemment, on obtient une bijection de N dans Z × N^∗. La représentation d'un rationnel par une fraction n'est pas unique, mais, sachant que Q est infini, on en déduit facilement une définition par récurrence d'une bijection de N dans Q (on prend pour image de n le quotient du premier couple dans l'énumération de Z × N^∗ qui fournit un rationnel non encore énuméré). C'est également une conséquence du théorème de Cantor-Bernstein, simple cependant à démontrer dans ce cas particulier.

Autres exemples

Les deux premiers exemples, dénombrabilité de Z, mais surtout dénombrabilité de N × N, utilisent un argument assez générique pour des démonstrations de dénombrabilité : on énumère les éléments de l'ensemble considéré par blocs successifs, de taille constante dans le cas de Z — deux éléments de même valeur absolue, de taille croissante dans le cas N × N — les diagonales, c'est-à-dire les couples de même somme. On a également une façon uniforme d'ordonner, donc d'énumérer, chaque bloc fini.

• Par exemple l'ensemble des mots sur un alphabet fini, c'est-à-dire des suites finies (de longueur arbitrairement grande) d'éléments d'un ensemble fini, est dénombrable. On l'énumère par blocs de mots de taille fixe, d'abord le mot vide, puis les mots de taille 1, puis ceux de taille 2, etc. Chaque bloc peut-être ordonné lexicographiquement, à partir d'un ordre arbitraire sur l'alphabet de départ.
• De la même façon l'ensemble des suites finies d'entiers (cela revient à prendre des mots sur un alphabet dénombrable), est dénombrable. On peut utiliser pour bloc les suites de longueur plus petite ou égale à n d'entiers plus petits ou égaux à n où n apparait nécessairement si la suite est de longueur strictement inférieure à n-1. Chaque bloc s'ordonne lexicographiquement.
• L'ensemble des polynômes à coefficients entiers naturels peut être vu comme l'ensemble des suites (finies) de ces coefficients. Ce sont toutes les suites finies d'entiers dont le dernier terme est non nul. De façon strictement analogue au cas précédent, cet ensemble est dénombrable. Comme l'ensemble des entiers relatifs Z est dénombrable, par composition, on en déduit que l'ensemble des polynômes à coefficients entiers relatifs est également dénombrable.

• L'ensemble des nombres algébriques (réels ou complexes) est donc également dénombrable : puisque l'on peut énumérer les polynômes à coefficients entiers, et que chacun de ces polynômes a un nombre fini de racines, on peut énumérer les nombres algébriques, polynôme par polynôme, en ne considérant que les racines du polynôme qui ne sont pas déjà apparues dans l'énumération. Comme ni l'ensemble des réels ni l'ensemble des complexes ne sont dénombrables, on en déduit l'existence de nombres (réels ou complexes) transcendants.

On pourra également utiliser pour ces derniers exemples les théorèmes généraux qui seront vus dans la suite.