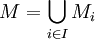Théorème de Hahn-Banach - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus particulièrement en analyse et en géométrie, le théorème de Hahn-Banach, dû aux deux mathématiciens Hans Hahn et Stefan Banach, garantit l'existence d'une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l'espace, mais limitées partout).
En permettant de prouver abstraitement l'existence de nombreuses fonctions continues, c'est un outil fondamental de l'analyse fonctionnelle.
Par son interprétation géométrique en termes d'hyperplans évitant un convexe fixé, il joue également un rôle primordial dans l'étude de la géométrie des convexes, et au-delà en analyse convexe.
Forme analytique et forme géométrique
Les énoncés dénommés « théorème de Hahn-Banach » dans la littérature scientifique sont nombreux, différant les uns des autres parfois par de simples détails et parfois de façon significative. Ils se divisent néanmoins nettement en deux classes : certains garantissent de pouvoir prolonger une forme linéaire, sous certaines exigences de majoration (les formes « analytiques » du théorème) ; d'autres assurent qu'on peut séparer deux ensembles convexes par un hyperplan affine (les formes « géométriques » du théorème).
Donnons pour commencer un exemple d'énoncé pour chacune de ces deux catégories.
Un énoncé de la forme analytique du théorème
Théorème — Soit V un espace vectoriel sur

Soit G un sous-espace vectoriel de V, et f une forme linéaire sur G qui y vérifie en tout point la condition de majoration :
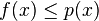
Il existe alors un prolongement de f en une forme linéaire sur l'espace V tout entier, vérifiant encore la condition :
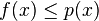
Un énoncé de la forme géométrique du théorème
Théorème — Soit E un espace vectoriel topologique et C un convexe ouvert non vide de E.
Soit L un sous-espace affine de E qui vérifie la condition :
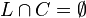
Il existe alors un hyperplan affine H contenant L et qui vérifie lui aussi la condition :
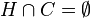
De plus, H est un hyperplan fermé.
La forme analytique du théorème est due à Banach (1932) généralisant un résultat de Hahn qui s'intéresse dès 1920 aux espaces vectoriels normés. Il existe une généralisation du théorème de Hahn-Banach aux espaces vectoriels sur le corps des complexes due à Bohnenblust et Sobczyk (1938). Les difficultés de la généralisation du théorème de Hahn-Banach apparaissent même pour des espaces vectoriels de dimension finie.
Relations entre les deux énoncés et preuve de la forme « géométrique »
La forme géométrique du théorème —d'où on peut ensuite déduire une succession de variantes diverses relatives à la séparation des convexes— est la retranscription de la forme analytique pour le cas particulier où la fonction convexe qui y intervient est la jauge d'un ouvert convexe d'un espace normé. C'est d'ailleurs le cas dans les utilisations les plus simples et fondamentales du théorème en analyse fonctionnelle qu'on peut selon ses goûts lire depuis une version ou l'autre (on en verra un exemple plus bas).
Voyons de plus près comment la forme géométrique se déduit de la forme analytique :
Quitte à faire préalablement une translation, on supposera que l'origine est dans C. Dès lors, puisque L ne rencontre pas C, c'est donc un sous-espace affine évitant l'origine.
Notons p la jauge du convexe C. Elle est sous-linéaire et donc convexe comme toute jauge ; par définition même d'une jauge il est évident que pour tout x dans C,
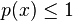
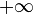
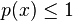
Notons G le sous-espace vectoriel engendré par L. Puisque
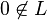
Enfin, pour x dans L,
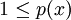
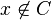
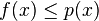
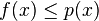
Toutes les hypothèses de la version dite « analytique » du théorème sont en place. Appliquons la donc. Elle nous offre une nouvelle forme linéaire encore notée f, cette fois définie sur E tout entier. Notons H l'hyperplan affine d'équation f(x) = 1 : par construction, c'est bien un hyperplan contenant L.
Soit maintenant un point x de C : pour ce point,
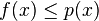
Enfin les hyperplans d'un espace vectoriel topologique sont nécessairement fermés ou denses. Or H n'est pas dense puisqu'il ne rencontre pas le voisinage C de 0. C'est donc qu'il est fermé.
On peut s'étonner que la forme géométrique fasse intervenir une topologie tandis que la forme analytique concerne un espace vectoriel sans structure additionnelle. En fait, il est tout à fait possible d'énoncer une forme géométrique dans un espace vectoriel quelconque : il faudra alors supposer que tout translaté du convexe C contenant l'origine est absorbant, à défaut de pouvoir donner un sens à « ouvert » ; on n'a bien sûr plus le complément sur le caractère fermé de l'hyperplan obtenu tombe. La démonstration est la même.
La preuve de la forme « analytique »
Deux types d'idées bien distinctes sont à mettre bout à bout pour aboutir à une preuve dans le cadre de généralité où le théorème a été énoncé. Dans un premier temps, quelques calculs assez simples permettent de justifier l'extension de la forme linéaire f dans le cas particulier où G est de codimension 1 dans V. Une fois cette étape franchie, on a déjà le théorème en dimension finie (il suffit de faire grossir pas à pas le sous-espace où on a réussi à étendre f, d'une dimension à chaque pas, et jusqu'à atteindre la dimension de V). En revanche, pour les usages en dimension infinie, il faut adapter cette méthode fort simple d'avancée méthodique et appeler quelques techniques assez standardisées de théorie des ensembles : on exécute ainsi une récurrence transfinie, le plus souvent rédigée sous forme d'un appel au lemme de Zorn.
Première partie : gagner une dimension
Dans un premier temps, on va prolonger la forme linéaire f à un espace plus grand que G en gagnant une dimension. Prenons un élément v0 de V en dehors de G (s'il n'y en a pas G = V et on a terminé avant même d'avoir commencé).
Le prolongement de f au sous-espace vectoriel
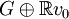
dans laquelle α est un réel qu'il va falloir choisir judicieusement pour que la condition de majoration de f reste vérifiée dans
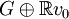
Il est clair que cette méthode d'extension fournit une forme linéaire, quel que soit le choix de α.
La condition de majoration sera vérifiée si et seulement si, pour chaque x de G et chaque λ réel, l'inégalité suivante est vérifiée :
-
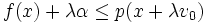
Après avoir noté que pour λ = 0 elle est justifiée par hypothèse, on peut ne s'intéresser qu'aux contraintes correspondant à
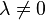
-
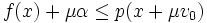
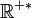
-
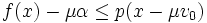
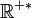
Des manipulations élémentaires permettent de les regrouper sous la forme :
Notons
![a_{x,\mu} = {1\over\mu}\left[f(x)-p(x-\mu v_0)\right]](https://static.techno-science.net/illustration/Definitions/autres/7/7c6767a3fe78c1948e485069d1b4956e_52c3249276d5c471baddb45f722ca32e.png)
![b_{x,\mu} ={1\over\mu}\left[p(x+\mu v_0)-f(x)\right]](https://static.techno-science.net/illustration/Definitions/autres/0/009a6e5bd0aa2a4b5e8fd68ee319d1bd_fb9ec94fd5d67cd1cd0b7f4aa2ca6daf.png)
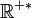
- pour tout
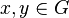
 .
.
Mais cette condition est réalisée, par une vérification lourde mais facile qui exploite la convexité de p, la linéarité de f et la majoration supposée vraie sur G : en effet, pour x, y dans G et tous μ,ν > 0:
-
![b_{y,\nu} - a_{x,\mu} = {1\over\nu}\left[p(y+\nu v_0)-f(y)\right] - {1\over\mu}\left[f(x)-p(x-\mu v_0)\right]](https://static.techno-science.net/illustration/Definitions/autres/2/2077d5bb4c374fd8e14ab94f1e3fafc7_b2a62f879a00582a3b5a7a9483932981.png)
-
![={{\mu+\nu}\over{\mu\nu}}\left[{\nu\over{\mu+\nu}}p(x-\mu v_0)+{\mu\over{\mu+\nu}}p(y+\nu v_0)-{\nu\over{\mu+\nu}}f(x)-{\mu\over{\mu+\nu}}f(y)\right]](https://static.techno-science.net/illustration/Definitions/autres/7/7088652ed1c5ea76fc1f1fd09d4adf5f_c1a16f0b28dc6e0510967f385ab4a533.png)
-
![\geq{{\mu+\nu}\over{\mu\nu}}\left[p\left({\nu\over{\mu+\nu}}(x-\mu v_0)+{\mu\over{\mu+\nu}}(y+\nu v_0)\right)-f\left({{\nu x}\over{\mu+\nu}}+{{\mu y}\over{\mu+\nu}}\right)\right]](https://static.techno-science.net/illustration/Definitions/autres/1/1f5c334341b6cf6bd19016bc1cf0a0f9_0c5680dca3830fb825743a1e1ddc72f0.png)
-
![={{\mu+\nu}\over{\mu\nu}}\left[p\left({{\nu x+\mu y}\over{\mu +\nu}}\right)-f\left({{\nu x+\mu y}\over{\mu +\nu}}\right)\right]\geq 0](https://static.techno-science.net/illustration/Definitions/autres/5/55e08b049880550c1abe845ea88923d8_06d85c917e087e72d516fddca7079e80.png)
Deuxième partie : exécution d'une récurrence transfinie
En raisonnant de proche en proche, on voit que l'on peut prolonger f à des espaces de plus en plus grands. Si G est de codimension finie dans V, alors le procédé ainsi défini s'arrête. Sinon, on utilise l'axiome du choix.
Pour cela, on considère l'ensemble des couples (M,g) dans lesquels M est un sous-espace vectoriel de V contenant G et g est une forme linéaire sur M prolongeant f (en respectant la contrainte de majoration par p), et on l'ordonne partiellement par :
-
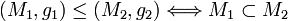
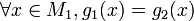
L'ensemble des couples est inductif. En effet si
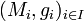
M est un sous-espace vectoriel. (En général, une union d'espaces vectoriels n'est pas un espace vectoriel, en revanche, ici, c'est le cas car la famille des
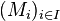
On définit la forme linéaire g sur l'espace M par :
- g(x) = gi(x) si
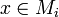
On vérifie aisément que cette définition de g est correcte. (M, g) est alors un majorant de la chaîne
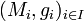
Maintenant si N n'est pas égal à V, alors la première partie de la démonstration montre que l'on peut prolonger f (définie sur N) à un espace strictement plus grand que N, ce qui en contradiction avec la maximalité de N.
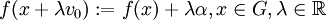
![{1\over\mu}\left[f(x)-p(x-\mu v_0)\right]\leq \alpha \leq {1\over\mu}\left[p(x+\mu v_0)-f(x)\right].](https://static.techno-science.net/illustration/Definitions/autres/5/5f27220431653b286a094aba5db87128_6ced0ca95580ff68b8b897ca8454e20f.png)