Axiome du choix - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Énoncé - Particularités - Énoncés équivalents - Exemples où l'axiome du choix est nécessaire - Anecdote - Formes faibles de l'axiome du choix

Introduction

En mathématiques, l'axiome du choix, abrégé en « AC », est un axiome de la théorie des ensembles.

Énoncé

L'axiome du choix peut s'énoncer comme suit :

« Étant donné un ensemble X d'ensembles non vides, il existe une fonction définie sur X, appelée fonction de choix, qui à chacun d'entre eux associe un de ses éléments. »

L'appel à l'axiome du choix n'est pas nécessaire si X est un ensemble fini. L'axiome du choix devient, dans ce cas particulier, une simple conséquence de la définition d'ensemble non vide (c'est-à-dire qu'il existe un élément appartenant à cet ensemble). Le résultat se montre par récurrence sur le nombre d'éléments de X.

Il existe d'autres cas particuliers, où une telle fonction peut être explicitement définie. Par exemple, pour un ensemble X de sous-ensembles non vides des entiers naturels, on peut définir une fonction de choix en posant, pour x un élément de X, f(x) égal à l'élément minimal de x. On s'est servi de la propriété de bon ordre sur les entiers naturels, et non de l'axiome du choix. Cependant dans le cas général, l'existence d'une fonction de choix repose sur l'axiome ci-dessus.

Autres formulations

On trouve d'autres formulations de l'axiome du choix, très proches de la précédente, dont les suivantes :

(1) « Le produit d'une famille d'ensembles non vides est non vide », c'est-à-dire que pour toute famille (X_i)_{i ∈ I} :

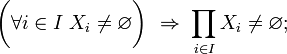
Ce premier énoncé est équivalent à l'axiome du choix, car un élément de ce produit est par définition une fonction de choix définie sur l'ensemble {X_i | i ∈ I} des éléments de la famille.

(2) Étant donné un ensemble E, il existe une fonction définie sur l'ensemble des parties de E, et qui à toute partie non vide de E associe un élément de cette partie.
(3) « Toute surjection est inversible à droite » ;
(4) Pour toute relation d'équivalence R sur un ensemble X, il existe un choix de représentants de R, autrement dit un sous-ensemble Y de X tel que tout élément de X est R-équivalent à un unique élément de Y.

Le deuxième énoncé est équivalent à l'axiome du choix.

Le deuxième énoncé est un cas particulier de l'énoncé original, modulo un prolongement arbitraire de la fonction de choix pour l'ensemble vide. On déduit l'énoncé original du deuxième, en prenant comme ensemble E la réunion des ensembles du X de l'énoncé original. Le second énoncé fournit une fonction de choix sur l'ensemble des parties non vides de E, donc sur X, sous-ensemble de celui-ci.

Le troisième énoncé est équivalent au premier (donc à l'axiome du choix).

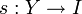
Pour (X_i)_{i ∈ I} une famille d'ensembles non vides, notons Y la réunion disjointe des X_i, c'est-à-dire l'ensemble de tous les couples (i,x) tels que x appartienne à X_i. Alors la première projection, de Y dans I, qui à (i,x) associe i, est une surjection, dont tout inverse à droite fournit un élément du produit des X_i. Réciproquement, si $s:Y\rightarrow I$ est une surjection alors, en notant X_i l'ensemble des antécédents de i par s, on constitue une famille (X_i)_{i ∈ I} d'ensembles non vides, et tout élément du produit de cette famille fournit un inverse à droite pour s.

Le quatrième énoncé est équivalent au troisième.

À toute relation d'équivalence R, sur un ensemble Y, est naturellement associée une surjection s, de Y dans l'ensemble I des classes d'équivalence. Inversement, à toute surjection s, de Y dans un ensemble I, est naturellement associée une relation d'équivalence sur Y : deux éléments sont équivalents s'ils ont même image par s. Un inverse à droite pour s est exactement un choix d'un ensemble de représentants de R.