Base (algèbre linéaire) - Définition
La liste des auteurs de cet article est disponible ici.
Base d'un espace dual
Soit E un K-espace vectoriel. L'ensemble des formes linéaires sur E forment un K-espace vectoriel appelé espace dual de E noté E * . Si E est de dimension finie, alors E * est aussi de dimension finie et sa dimension est égale à celle de E. Ils sont donc isomorphes.
Si
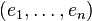

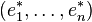
où δij est le symbole de Kronecker.
La famille de formes linéaires
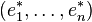
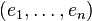
Inversement, si
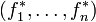
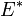
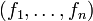
La base
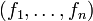
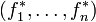
Base d'un module
Un module est une structure algébrique identique à celle d'espace vectoriel à la différence près que l'ensemble des scalaires ne forment plus un corps mais un anneau.
Certaines propriétés vraies pour les espaces vectoriels ne sont plus vraies pour les modules. Par exemple l'existence d'une base n'y est plus assurée, et on ne peut pas nécessairement y développer de théorie de la dimension, même dans un module engendré par un nombre fini d'éléments.
Cependant, on peut quand même définir une notion de base, identique à celle des espaces vectoriels. Un module qui possède une base s'appelle un module libre.