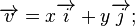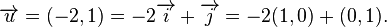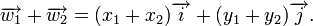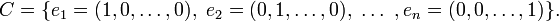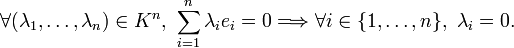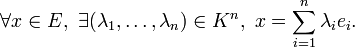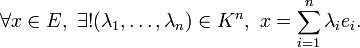Base (algèbre linéaire) - Définition

Introduction

En mathématiques, et plus particulièrement en algèbre linéaire, une base d'un espace vectoriel est une famille de vecteurs de cet espace telle que chaque vecteur de l'espace puisse être exprimé de manière unique comme combinaison linéaire de vecteurs de cette base. En d'autres termes, une base est une famille de vecteurs à la fois libre et génératrice d'un espace vectoriel.

Introduction géométrique

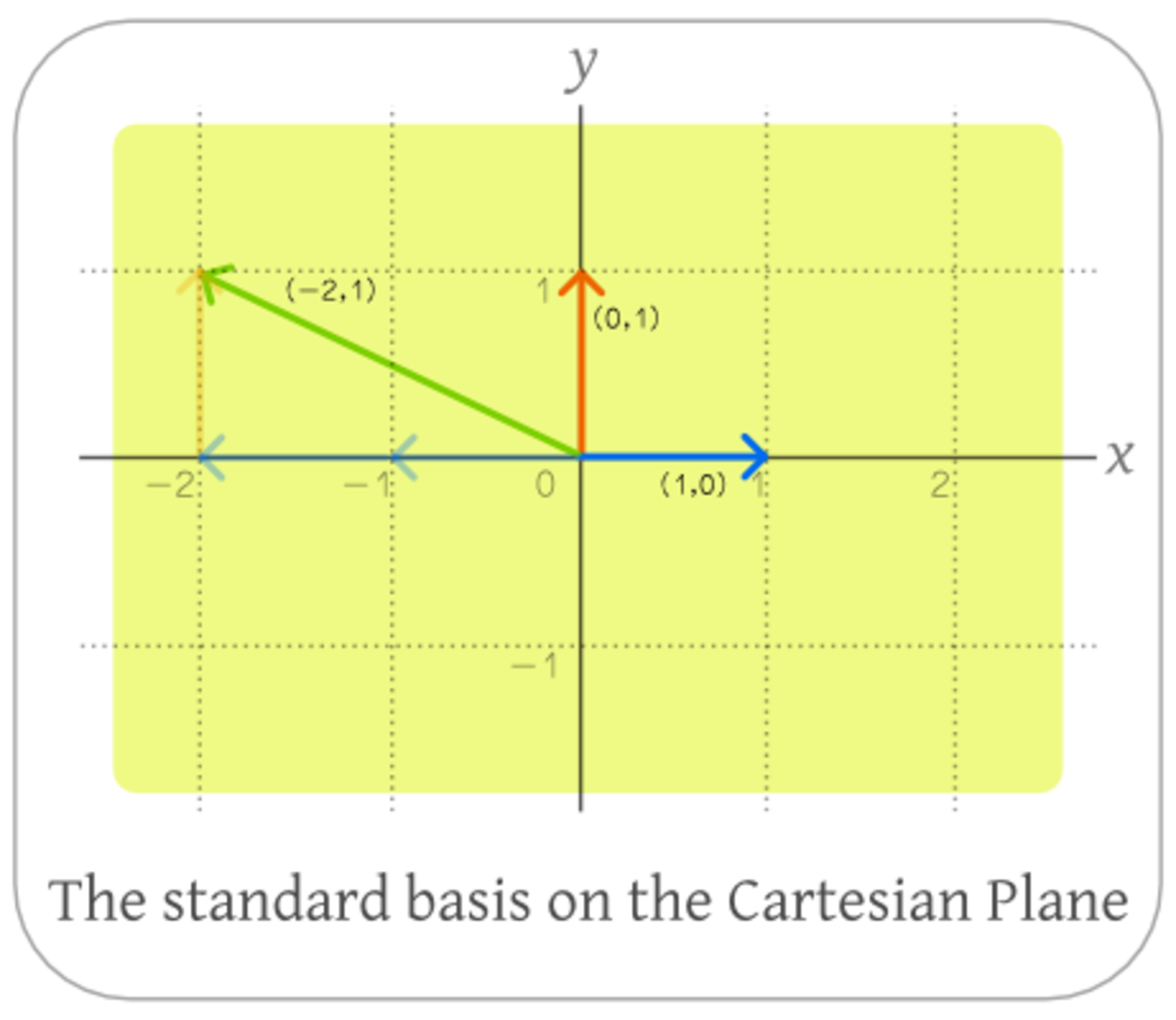
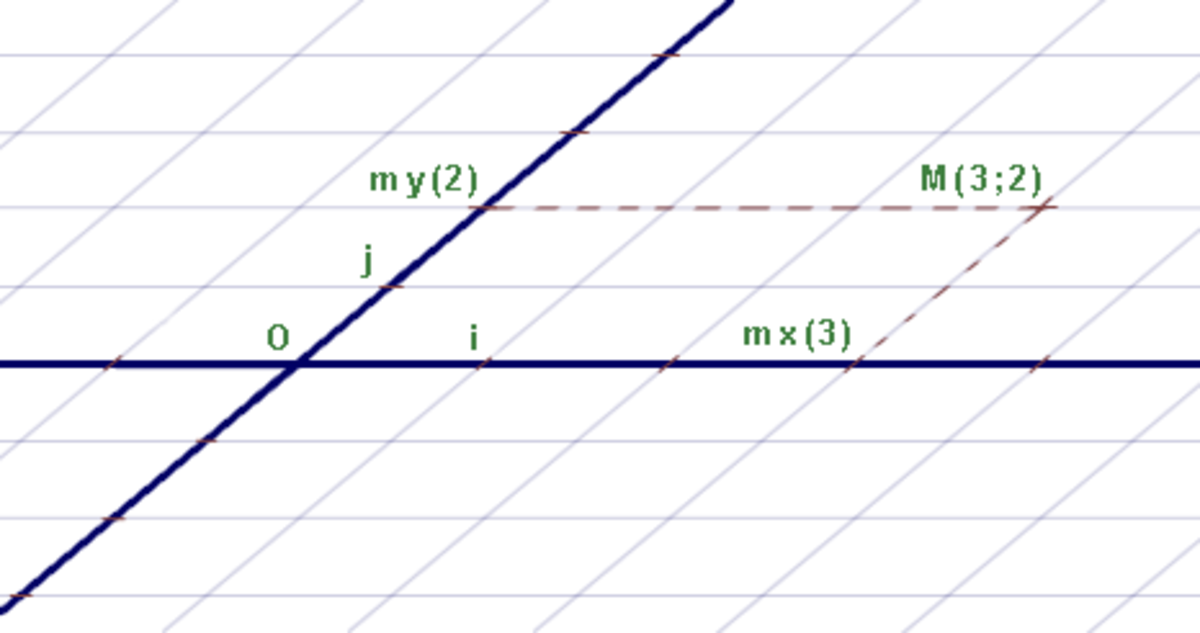
La géométrie plane, celle d'Euclide, peut comporter une approche algébrique, celle de Descartes. En utilisant les coordonnées cartésiennes, on peut identifier un vecteur du plan à un couple de réels. Par exemple, la figure montre comment placer le vecteur . On se sert alors des deux vecteurs de référence (dessinés en rouge et bleu) pour le dessiner. Ainsi, tous les vecteurs du plan peuvent être exprimés de manière unique en termes de nombres vis-à-vis de deux vecteurs de référence. Ces deux vecteurs sont appelés base canonique du plan. En les notant respectivement et , un vecteur quelconque du plan s'exprime comme combinaison linéaire de ces deux vecteurs:

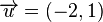
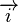
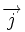
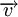
où x et y sont des nombres réels. Par exemple,

Cette écriture permet d'effectuer des calculs simplement. Par exemple, on peut additionner deux vecteurs et (où x₁, x₂, y₁ et y₂ sont des réels) de la façon suivante:

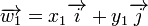
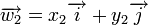
Cette addition a une signification géométrique. Ainsi, il existe des connexions entre géométrie et calcul algébrique.

Cette base n'est pas unique. En fait, n'importe quel couple de vecteurs du plan choisi au hasard forme une base, à condition que les deux vecteurs ne soient pas colinéaires (c'est-à-dire qu'il s'agit d'une famille libre). Les deux vecteurs peuvent alors être utilisés pour exprimer tous les autres vecteurs (c'est-à-dire qu'il s'agit d'une famille génératrice). La décomposition selon ces deux vecteurs est alors unique. La figure ci-contre montre une autre base du plan. Travailler dans d'autres bases que la base canonique permet de simplifier grandement les calculs, si la base choisie est adaptée au problème.

Cette notion de base se généralise à toute structure vectorielle. Cela permet les mêmes avantages que pour les bases du plan, à savoir un cadre simple dans lequel tout vecteur possède une unique écriture, qui facilite les calculs dans cette structure.

Exemples

• Le -espace vectoriel admet une base C particulière, appelée base canonique, définie par

La dimension de est donc n.

• L'espace vectoriel des matrices d'ordre à coefficients dans un corps K admet pour base l'ensemble formée des matrices élémentaires de , c'est-à-dire des matrices ayant un coefficient égal à 1 et tous les autres nuls. La dimension de est donc np.

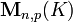
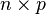
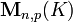
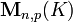
• L'espace vectoriel des polynômes sur un corps K admet pour base Ou plus généralement, toute famille de polynômes étagée en degré convient. La dimension de K[X] est donc infinie.

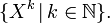
Définition formelle

Soit E un espace vectoriel sur un corps K.

Famille libre

Une famille finie de vecteurs de E est dite libre dans E si, et seulement si:

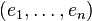
Dans le cas contraire, elle est dite liée.

Plus généralement, si est une famille (éventuellement infinie) de vecteurs de E, cette famille est dite libre dans E si, et seulement si, toutes ses sous-famille finies sont libres dans E.

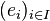
Famille génératrice

Une famille finie de vecteurs de E est dite génératrice de E si, et seulement si, tout vecteur de E est une combinaison linéaire des vecteurs de cette famille :

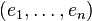
Plus généralement, si est une famille (éventuellement infinie) de vecteurs de E, cette famille est dite génératrice de E si, et seulement si, tout vecteur de E est une combinaison linéaire d'une partie finie de la famille .

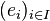
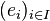
Définition

Une famille de vecteurs de E est une base de E si, et seulement si, c'est une famille à la fois libre dans E et génératrice de E. De façon équivalente, une famille est une base de l'espace vectoriel E quand tout vecteur de l'espace se décompose de façon unique en une combinaison linéaire de vecteurs de cette base.

On précise cette dernière caractérisation. Une famille finie est une base de E si et seulement si :

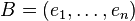
Plus généralement, si est une famille (éventuellement infinie) de vecteurs de E, cette famille est une base de E si, et seulement si, et pour tout vecteur x de E, il existe une unique famille de scalaire qui est nulle sauf en un nombre fini d'indices et telle que :

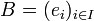
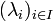
Les scalaires λ_i sont appelés coordonnées du vecteur x dans la base B.

Dimension

Qu'elles soient finies ou non, toutes les bases d'un espace vectoriel E ont la même cardinalité, appelée la dimension de E. En particulier, si E admet une famille génératrice finie, toute base de E est finie, et la dimension de E est le nombre de vecteurs qu'elle comprend. Ce résultat, qui justifie la définition de la dimension, porte des noms différents selon les auteurs : théorème de la dimension, théorème d'équicardinalité des bases, etc.

Toute famille libre de E a alors un cardinal inférieure ou égal à dim(E), et toute famille génératrice de cet espace a un cardinal supérieur ou égal à dim(E).

Par exemple, Kⁿ est de dimension n car sa base canonique possède exactement n vecteurs. Les solutions à l'équation différentielle linéaire f'' + hf' + k = 0 forment un espace vectoriel réel de dimension 2 : ce résultat s'appuie sur le théorème de Cauchy Lipschitz.