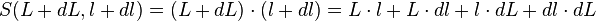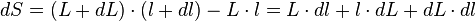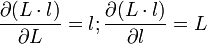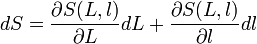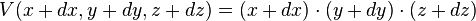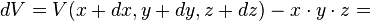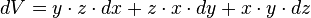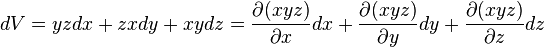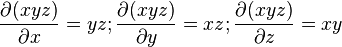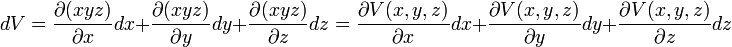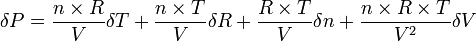Calcul d'incertitude - Définition
La liste des auteurs de cet article est disponible ici.
Utilisation des différentielles totales exactes
Une loi physique s'exprime par une relation algébrique entre un certain nombre de grandeurs mesurables.
Exemples simples : surface et volume
Le calcul de la surface d'un rectangle de côtés L et l :
devient lorsque les côtés deviennent L+dL et l+dl:
Donc la variation de la surface dS peut s'écrire :
que l'on approche par :
-
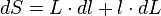
Noter que
d'où
De même la variation de volume d'une boîte de côtés x, y, z de volume V=xyz :
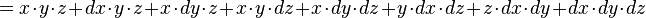
peut s'écrire
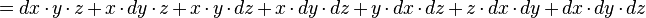
que l'on approche par :
Noter que :
car
et donc
La variation d'une fonction f(x,y,z)
Et plus généralement, pour le calcul de la variation d'une fonction f(x,y,z).
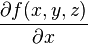
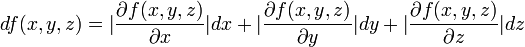
Loi des gaz parfaits
Prenons par exemple la loi des gaz parfaits reliant :
- P : la pression du gaz
- V : le volume occupé par le gaz
- n : la quantité de gaz en moles (1 mole = 6,022 1023 molécules)
- R : la constante des gaz parfaits = 8,314 J.K-1.mol-1
- T : la température absolue du gaz, en kelvin.
-
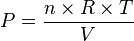
Écrivons sa différentielle :
-
![\begin{array}{rcl} dP (T,R,n,V) & = & P (T+dT,R+dR,n+dn,V+dV)-P (T,R,n,V)\\[2ex] ~ & = & \displaystyle{\frac{n \times R}{V} dT + \frac{n \times T}{V} dR + \frac{ R \times T}{V}dn - \frac{n \times R \times T}{V^2}dV} \end{array}](https://static.techno-science.net/illustration/Definitions/autres/d/d95aa0abd0520b768ab356cf2fe5e4f6_a56478436d96704ce8b13c8a85141d3c.png)
![\begin{array}{rcl} dP (T,R,n,V) & = & P (T+dT,R+dR,n+dn,V+dV)-P (T,R,n,V)\\[2ex] ~ & = & \displaystyle{\frac{n \times R}{V} dT + \frac{n \times T}{V} dR + \frac{ R \times T}{V}dn - \frac{n \times R \times T}{V^2}dV} \end{array}](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d95aa0abd0520b768ab356cf2fe5e4f6_a56478436d96704ce8b13c8a85141d3c.png)
la variation la plus grande s'obtiendra lorsque les 4 termes ci-dessus s'ajouteront :
donne l'erreur absolue sur P déduite du calcul de P à partir de la connaissance des erreurs sur T, R, n et V.
Dans ce cas particulier, on a :
-
-
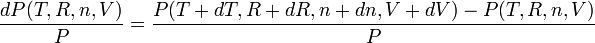
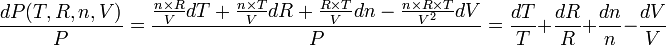
et donc dans l'absolu :
-
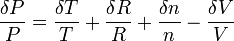
On peut aussi utiliser la différentielle logarithmique :
-
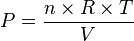
Donc
-
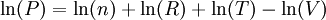
En dérivant, on obtient :
-
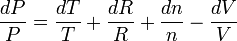
Cette méthode plus rapide s'applique lorsqu'on cherche à faire la différentielle d'une fonction, quotient ou produit de plusieurs variables.
Les incertitudes relatives s'ajoutent lorsque l'on a un produit de variables et ce résultat est remarquable car il est facile à retenir : les incertitudes relatives s'ajoutent lorsque la formule ne comporte que des produits (au sens large : une division est un produit par l'inverse).
