Caractère d'un groupe fini - Définition

Cas commutatif

Dans le cas où G est commutatif, le groupe dual possède une propriété intéressante, il est isomorphe à G, ce qui permet simplement de construire une analyse harmonique sur G.

Groupe cyclique

Dans ce pararagraphe le groupe cyclique d'ordre g est noté C_g et ω désigne une racine primitive g-ième de l'unité, c'est-à-dire un générateur du groupe des racines g-ièmes de l'unité. Le symbole 1_C désigne ici un générateur du groupe C_g et si s est un entier compris entre 0 et g - 1, alors s_C désigne la valeur s.1_C.

Un cas simple d'analyse du groupe dual correspond au groupe cyclique, il est décrit par les propositions suivantes :

• Pour tout caractère χ de C_g, il existe un entier i compris entre 1 et g - 1 tel que l'égalité suivante est vérifiée :

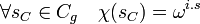
• Réciproquement, si i est un entier compris entre 1 et g - 1 et si χ_i est l'application définie par l'égalité suivante, alors χ_i est un caractère de C_g.

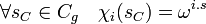
• Si i est un entier compris entre 1 et g - 1, alors l'application de C_g dans son dual, qui à i_C associe χ_i est un isomorphisme de groupe.

• Pour tout caractère χ de C_g, il existe un entier i compris entre 1 et g - 1 tel que l'égalité suivante est vérifiée :

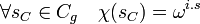
χ(1_C) est une racine de l'unité et ω est une racine primitive, il existe donc un entier i compris entre 1 et g - 1 tel que χ(1_C) est égal à ωⁱ. Les propriétés de morphisme de χ montre l'égalité suivante, ce qui permet de conclure :

• Si i est un entier compris entre 1 et g - 1 et si χ_i est l'application définie par l'égalité suivante, alors χ_i est un caractère de C_g.

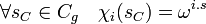
Il suffit de vérifier que χ_i est bien un morphisme de groupe. Cette propriété découle des égalités suivantes :

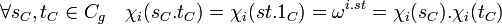
• Si i est un entier compris entre 1 et g - 1, alors l'application φ de C_g dans son dual, qui à i_C associe χ_i est un isomorphisme de groupe.

Vérifions que l'application φ est un morphisme :

Le noyau de φ est réduit à l'élément neutre, l'application est donc injective, de plus les deux propositions précédentes montre que l'ordre du groupe dual est égal à g, le cardinal de C_g, l'application est donc surjective, ce qui termine la démonstration.

 

Groupe abélien

Les résultats du paragraphe précédent se généralisent à tous les groupes abéliens finis:

• Le dual d'un groupe abélien fini G est isomorphe à G.

Ce résultat découle du fait qu'un groupe abélien fini est un produit de groupes cycliques et de la proposition suivante :

• Soit H et K deux groupes abéliens, le dual du produit direct de H et de K est isomorphe au produit des duals de H et de K.

• Soit H et K deux groupes abéliens, le dual du produit direct de H et de K est isomorphe au produit des duals de H et de K.

Notons i_H (resp. i_K) le morphisme canonique de H (resp. K) dans HxK. Considérons alors le morphisme ψ du dual de HxK dans le produit des duals défini par :

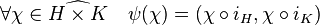
L'application ψ est un morphisme injectif, soit χ_H, χ_K deux éléments des duals de H et de K. On remarque que l'application χ_HxK de HxK dans C^* définie par :

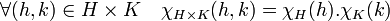
est un caractère de HxK antécédent de (χ_H, χ_K). L'application ψ est donc bien surjective. Ce qui termine la démonstration.

• Le dual d'un groupe abélien fini G est isomorphe à G.

Le théorème de structure des groupes abéliens finis (cf l'article associé) montre que G est isomorphe à un produit de groupe cycliques. Une récurrence sur le nombre de cycles et la proposition précédente permet alors de conclure.