Caractère d'un groupe fini - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un caractère d'un groupe fini est une notion associée à la théorie des groupes.
Un caractère d'un groupe fini G est un morphisme du groupe G dans C* le corps des nombres complexes non nuls.
Ce concept permet de définir le groupe dual de G, composé de l'ensemble des caractères de G. Il est à la base de l'analyse harmonique sur les groupes finis.
Cette notion correspond à un cas particulier de caractère d'une représentation d'un groupe fini.
Définitions et exemples
Définitions et premières propriétés
Dans tout l'article, G désigne un groupe fini d'ordre g, C le corps des nombres complexes et C* l'ensemble des nombres complexes non nuls. Sauf mention contraire, le groupe est noté multiplicativement et l'inverse d'un élément s de G est noté s-1. Le conjugué d'un nombre complexe z est noté z*.
-
- Un caractère de G est un morphisme du groupe G dans C*.
Un caractère correspond à un cas particulier de représentation d'un groupe fini, celui où l'espace vectoriel de la représentation est celui des nombres complexes. Dans ce contexte, un caractère est aussi le caractère d'une représentation au sens de la trace.
-
- Un caractère χ de G prend ses valeurs dans les racines g-ièmes de l'unité et vérifie l'égalité suivante :
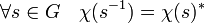
En effet, le théorème de Lagrange indique que si s est un élément de G, alors sg = 1, on en déduit que l'image de s par χ est une racine g-ième de l'unité et toute racine g-ième de l'unité admet pour inverse son conjugué.
-
- L'ensemble des caractères de G est appelé groupe dual de G et est généralement noté
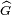
- L'ensemble des caractères de G est appelé groupe dual de G et est généralement noté
Le dual de G est naturellement munis d'une multiplication, celle des fonctions à valeur dans C :
-
- La multiplication confère au dual de G une structure de groupe abélien fini.
En effet, le dual de G est non vide car il contient au moins l'application qui à tout élément de G associe l'unité, ce caractère est l'élément neutre du groupe. L'associativité est une propriété générale de la multiplication des fonctions. Si χ est un caractère, l'application qui à tout élément de G associe le conjugué de χ est un caractère qui correspond à l'inverse de χ, tout élément du dual possède donc un symétrique. Enfin le corps des nombres complexes est commutatif, ce qui implque le caractère abélien du dual de G.
Un caractère est une application d'un ensemble de départ fini et son image, contenue dans le groupe des racines g-ièmes de l'unité est aussi fini, ce qui démontre que le dual est un groupe fini.
Premiers exemples
Considérons le cas ou G est le groupe symétrique d'indice n. L'application signature est un caractère à valeur dans {-1, 1}.
Si G est égal à Z/2.Z où Z désigne l'ensemble des entiers naturels, alors il existe deux caractères, celui qui à la classe de 1 associe 1 et celui qui associe -1.
Si G est égal à Z/3.Z, alors il existe trois caractères, défini par les trois valeurs que peuvent prendre l'image de la classe de 1 : 1, j ou j*. Ici j désigne la racine cubique de l'unité ayant une partie imaginaire positive.
Algèbre du groupe
Ici G désigne un groupe fini quelconque, C[G] désigne l'algèbre complexe du groupe G et (es) la base canonique de l'algèbre indexée par les éléments s de G.
L'algèbre du groupe G, noté ici C[G] est un espace vectoriel de base canonique indexée par G. Un élément du groupe dual de G se prolonge linéairement en un élément du dual de C[G] considéré comme un espace vectoriel. Il est donc possible d'identifier le groupe dual de G comme un sous-ensemble de l'espace dual de C[G].
Si C[G] est muni du produit hermitien canonique < | >, défini par la formule suivante, alors le dual de C[G] s'identifie avec l'algèbre du groupe, le groupe dual est donc identifié avec un sous-ensemble de C[G] :
![\forall x,y \in \mathbb C[G] \quad \exists (x_s)_{s \in G},(y_t)_{t \in G} \in \mathbb C^G \quad <x|y>=<\sum_{s \in G} x_s.e_s|\sum_{t \in G} y_t.e_t>=\frac 1g \sum_{s,t \in G} x_s^*.y_s \;](https://upload.wikimedia.org/math/c/d/9/cd975c5ff8ea5d6401cfd197afdba787.png)
-
- Le groupe dual de G est une famille orthonormale.
-
- Le groupe dual de G est élément du centre de l'algèbre du groupe G.
-
- Le groupe dual de G est une base de l'algèbre du groupe G si et seulement si G est un groupe abélien.
Ces trois propositions correspondent à des cas particuliers de la théorie des représentations d'un groupe fini, elles se démontrent simplement dans le cas présent :
-
- Le groupe dual de G est une famille orthonormale.
Soit χ un caractère du groupe G, alors χ*.χ = χ-1.χ = 1C[G] où 1C[G] désigne l'élément neutre de l'algèbre du groupe. On en déduit :

Si χ1 et χ2 sont deux caractères distincts de G. Notons χ le caractère χ1-1.χ2 alors :

Si t est choisi de tel manière à ce que χ(t) soit différent de 1, alors on en déduit que χ1 et χ2 sont orthogonaux.
-
- Le groupe dual de G est inclus dans le centre de l'algèbre du groupe G.
Il suffit pour cela de remarquer que tout caractère du groupe est une fonction centrale et que l'ensemble des fonctions centrales est le centre de l'algèbre.
-
- Le groupe dual de G est une base de l'algèbre du groupe G si et seulement si G est un groupe abélien.
Le groupe dual est une famille orthogonale, elle est donc libre. Si le groupe G est abélien, le groupe dual possède le même cardinal que le groupe G donc son ordre est celui de la dimension de l'algèbre du groupe.
Si le groupe G n'est pas abélien son algèbre associé ne l'est pas non plus, le groupe dual engendre un espace vectoriel inclus dans le centre de C[G] qui n'est pas égal à l'algèbre entière.
















































