Caractère d'un groupe fini - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Applications
Analyse harmonique sur un groupe abélien fini
Dans le cadre d'un groupe abélien fini, il est possible de définir la transformée de Fourier et le produit de convolution. La théorie de l'analyse harmonique est analogue à celle du corps des réels. On démontre l'égalité de Parseval, le théorème de Plancherel, la dualité de Pontryagin et la formule sommatoire de Poisson.
Bidual
Dans le cas où le groupe G est abélien, et de manière analogue à l'algèbre linéaire, il existe un isomorphisme canonique entre G et son bidual (c'est-à-dire le dual de son dual).
-
- L'application φ, définie par l'égalité suivante, est un isomorphisme entre G et son bidual :
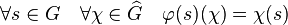
En effet, l'application φ est un morphisme injectif, l'égalité des cardinaux d'un groupe abélien et de son dual démontre la surjectivité et termine la démonstration.

















































