Code de Hamming (7,4) - Définition

Objectif

L'objectif du code est la transmission d'un message de quatre bits avec suffisamment de redondances pour que, même si une altération se produit, le récepteur soit capable de corriger automatiquement l'erreur. Le message envoyé est en conséquence plus long. Dans la pratique il contient sept bits, quatre composent le message et les trois autres servent à détecter et à corriger l'erreur, si nécessaire.

L'erreur que protège ce code est nécessairement limitée, si les sept bits transmis sont tous modifiés, il est vain d'espérer retrouver le message original. La protection contre la modification d'un unique bit est parfois largement suffisant, c'était le cas de la situation d'Hamming. Une modification d'un unique bit, c’est-à-dire d'un trou non lu sur la carte perforée ou d'une absence de trou considéré comme un trou est relativement rare. Supposons que cette situation se produit sur une série de quatre en moyenne une fois sur mille. Alors cinquante heures d'exécution de programme, qui utilisent par exemple de l'ordre de mille séries voit sa probabilité d'arrêt supérieure à soixante pour cent. La probabilité de trouver deux erreurs sur une série de sept est inférieur à un sur cinq cent mille. L'utilisation de mille séries de longueur sept possède une probabilité d'arrêt inférieure à deux pour mille dans le cas d'une utilisation de cinquante heures si les messages sont protégés par le code. C'était largement suffisant pour éradiquer la frustration d'Hamming.

Décodage

Matrice de contrôle

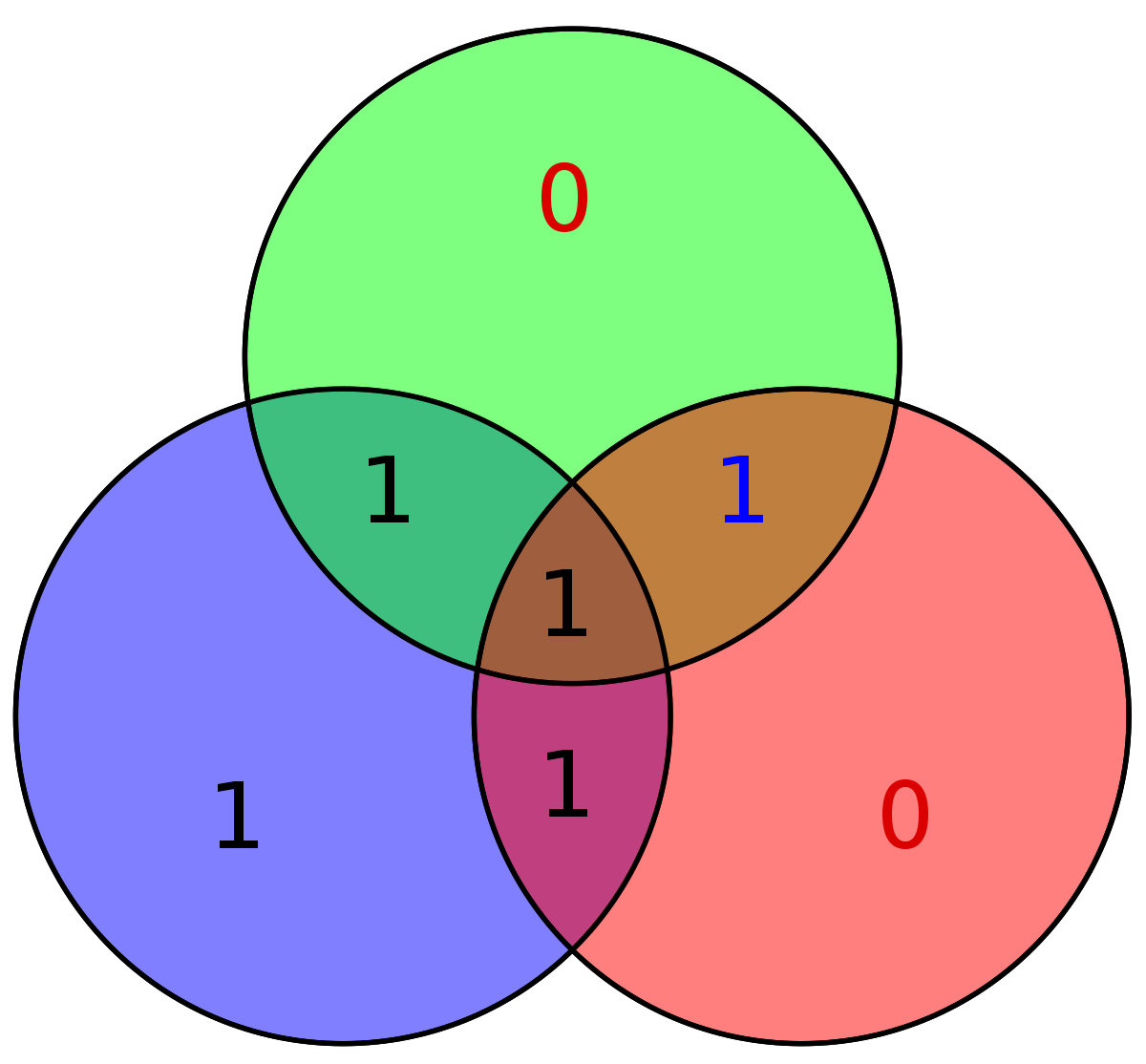
Le récepteur, sous réserve d'absence d'erreur peut facilement décoder le message c. Il sait que le code reçu : 0110011 contient les données en bleu, en position trois, cinq, six et sept. Il lui faut maintenant savoir si aucune altération n'a modifié le code reçu, ce qui correspond à l'un des rôles des bits de parité en rouge.

Une approche analogue à celle de l'encodage permet la détection d'erreur. Trois conditions doivent être remplies, une par cercle de la figure représentative. Chaque condition s'exprime comme une somme devant être paire, ou encore nulle dans le corps binaire. Ces trois conditions forment les trois lignes d'une matrice dite matrice de contrôle. Un message reçu est sans erreur si et seulement si le produit de la matrice de contrôle H par la matrice colonne C du vecteur c est égal à la matrice colonne nulle.

La condition associée au cercle rouge p₃ signifie que la somme p₃ + d₂ + d₃ + d₄ doit être paire. La première ligne de la matrice correspond aux coordonnées 0001111. Cette ligne correspond à la première ligne du tableau du paragraphe bit de parité. Il en est de même pour les autres lignes, correspondant aux cercles bleu et vert. On obtient la matrice H :

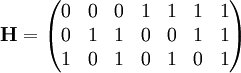
Il est possible de vérifier sur l'exemple que le produit de la matrice H par celle du mot du code c est bien nul. De manière plus générale, il est aussi possible de vérifier que le produit de H par G est bien nul, ce qui assure que tout message reçu est bien validé si aucune altération n'a été commise.

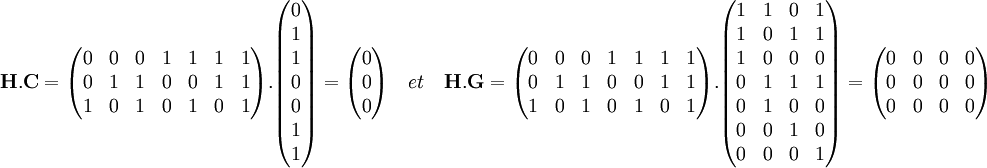
Correction d'erreur

Conséquence d'une erreur sur le bit d₂

L'objectif du code est la protection contre une erreur. Étudions le cas où le bit de donnée d₂ est altéré durant le transfert. Le message reçu n'est plus c = 0110011 mais x = 0110111. Deux conditions, correspondant au cercles rouge et verts, ne sont plus remplies. Le vecteur x ne peut passer le test de la matrice de contrôle :

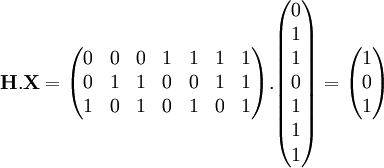
L'erreur est donc détectée, la matrice de contrôle présente un vecteur non nul, correspondant à la valeur cinq exprimée en binaire. La valeur de H.X est appelée syndrome. La correction associée correspond au mot e₅ composé de sept lettres égales à zéro sauf une, la cinquième est égale à un. Le décodage, dans le cas d'un syndrome non nul correspond à soustraire (ce qui revient à additionner dans un code binaire) l'erreur e₅ = 0000100. On obtient :

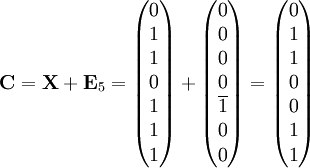
Quelle que soit l'erreur, à partir du moment où elle n'intervient que sur un bit, la matrice de contrôle fournit en binaire le numéro de la colonne fautive.

Une fois l'erreur corrigée, il est possible d'extraire les données et reconstruire le message initial. Une telle méthode est appelée décodage par syndrome.

Description du mécanisme

La linéarité de l'application associée à la matrice H filtre totalement le message pour proposer une image ne dépendant que de l'erreur :

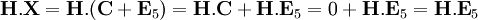
C'est la raison qui permet de parler de syndrome, il ne dépend que de l'erreur et non du message lui-même.

De plus, l'ordre de la base de F : p₁, p₂, d₁, p₃, d₂, d₃ et d₄, ainsi que celui des lignes de la matrice H ont été choisis de telle manière à ce qu'une lecture de gauche à droite correspondent à une liste de colonnes aux représentions binaires des nombres de un à sept ordonnées, l'image de e₅ par l'application est donc 101 et une telle propriété est vraie pour tous les e_i si i est un entier compris entre un et sept.