Code de Hamming (7,4) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le Code de Hamming (7,4) est un code correcteur linéaire binaire de la famille des codes de Hamming. À travers un message de sept bits, il transfère quatre bits de données et trois bits de parité. Il permet la correction de toute erreur portant sur un unique bit. C’est-à-dire que si, sur les sept bits transmis, un est altéré (un zéro devient un un ou l'inverse), alors il existe un algorithme permettant de corriger l'erreur, quel que soit le bit altéré.
Il fut introduit par Richard Hamming en 1950 dans le cadre de son travail pour les laboratoires Bell.
Histoire
Depuis 1946 Richard Hamming travaillait sur un modèle de calculateur à carte perforée de faible fiabilité. Si, durant la semaine, des ingénieurs pouvaient corriger les erreurs, les périodes chômées comme la fin de semaine voyaient les machines s'arrêter invariablement sur des bugs. La frustration d'Hamming le conduisit à inventer le premier code correcteur véritablement efficace.
Cette période correspond à la naissance de la théorie de l'information. Claude Shannon formalise cette théorie comme une branche des mathématiques. Hamming développe les prémisses de la théorie des codes et décrit sa solution comme un exemple.
Approche intuitive
Code parfait
La première question que l'on peut se poser est : combien d'informations la redondance doit-elle contenir? Ces informations sont contenues dans le message transmis par l'intermédiaire de p bits. Il existe donc quatre + p erreurs possibles, et en plus de ces informations il en faut une pour indiquer l'absence d'erreur. Cinq plus p informations doivent donc être stockées dans p bits. Or p bits peuvent au maximum contenir 2p informations. Cette situation est obtenue si chaque état décrit une information. On peut s'en rendre compte par un exemple, deux bits peuvent décrire quatre états : 00, 01, 10, 11 ce qui correspond à compter de zéro à trois en base deux. Si le code est idéal, p vérifie l'égalité 5 + p = 2p le terme de gauche décrit les informations nécessaire à la correction et celui de droite la quantité d'informations stockées dans les bits de parité. Cette équation admet une unique solution : p est égal à trois. Un code vérifiant ce type de propriété est dit parfait, l'article associé formalise cette approche.
Bit de parité
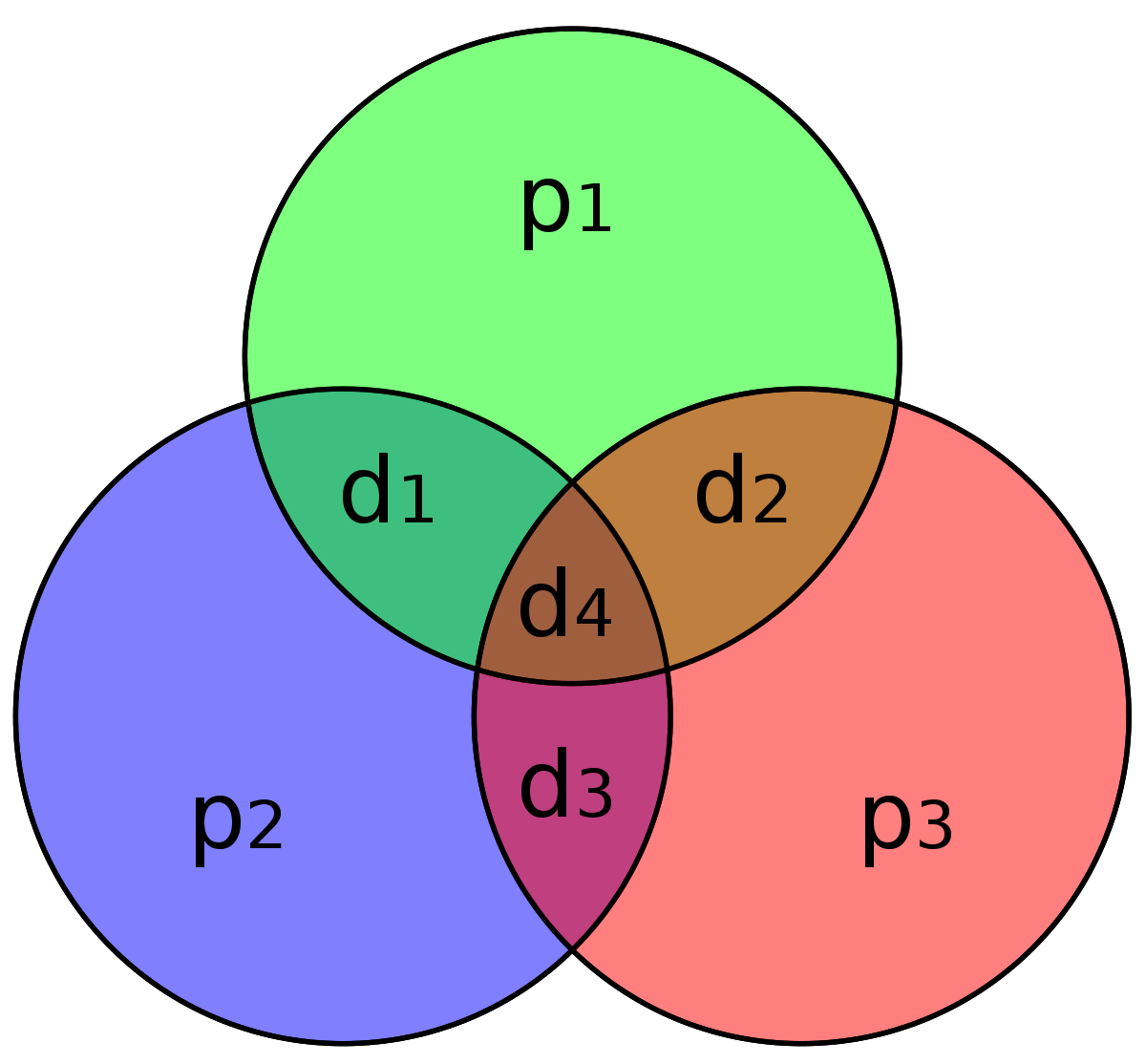
La figure de droite indique le mode de construction du code. Les valeurs d1, d2, d3 et d4 symbolisent les quatre bits du message. Les valeurs p1, p2, p3 correspondent aux bits de parité. Le bit p1 correspond à la parité du cercle vert, si d1 + d2 + d4 est pair p1 est égal à zéro, sinon p1 vaut un. En conséquence, si aucune altération ne se produit, la somme des bits du cercle vert est paire. Cette logique est poursuivie sur les cercles rouge et bleu.
Si une altération se produit par exemple sur p1 alors la parité du cercle de p1 est modifiée, en revanche celles des cercles de p2 et de p3 ne sont pas modifiées. Si la parité de d1 est modifiée, alors celles des cercles de p1 et de p2 le sont mais celle de p3 ne l'est pas. Le récapitulatif de la situation est donné dans le tableau suivant. Les sept colonnes correspondent aux sept possibles altérations des différents bits du message, les trois lignes correspondent aux parités des cercles associés. Si la parité du cercle est conservée alors la cellule associée est verte avec le texte oui, dans le cas contraire la cellule est rouge avec le texte non.
| Bit # | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| bit transmis | p1 | p2 | d1 | p3 | d2 | d3 | d4 |
| Cercle rouge | Oui | Oui | Oui | Non | Non | Non | Non |
| Cercle bleu | Oui | Non | Non | Oui | Oui | Non | Non |
| Cercle vert | Non | Oui | Non | Oui | Non | Oui | Non |
Si, par exemple les trois parités des trois cercles sont modifiées, alors il existe une erreur sur le bit d4. Pour chaque bit, une erreur engendre un jeu de parité différent. Si aucune erreur n'altère le message alors les trois parités sont à oui.
L'ordre des différentes colonnes n'est pas choisi au hasard. On remarque que si l'on transforme dans le tableau les Non en un et les Oui en zéro alors on obtient la suite des nombres de un à sept en binaire. Cette propriété permet par la suite un décodage aisé.

















































