Harmonique - Définition
Dans plusieurs domaines, une harmonique est un élément constitutif d'un phénomène périodique ou vibratoire (par exemple en électricité : les " courants harmoniques ", qui sont des perturbations du courant électrique industriel, dans le chemin de fer...).
Note : le mot " harmonique " s'utilise au féminin, mais également au masculin — plus rarement : 20% des utilisations. En physique, c'est le genre masculin qui est le plus utilisé.
En musique, une harmonique est une composante à part entière d'un son musical. Il s'agit d'une fréquence multiple de la fréquence fondamentale.
Mathématiques
L'adjectif harmonique est utilisé pour caractériser certaines fonctions ayant des propriétés de régularité et satisfaisant certaines Équations aux dérivées partielles.
Physique
Un harmonique est l'élément de décomposition primaire d'une fonction périodique exprimé dans la base de Hilbert.
En d'autres termes, un harmonique correspond à une fonction trigonométrique sinusoïdale (sinus ou cosinus) dont la fréquence est un multiple de la fréquence de la fonction périodique décomposée. La somme infinie de tous les harmoniques d'une fonction périodique reconstitue la fonction.
-
- Comme un signal périodique peut se décomposer en une somme de sinus et cosinus dont les fréquences sont des multiples de la fréquence du signal (dite fréquence fondamentale), le " poids " de certains harmoniques dans la décomposition spectrale d'un son correspond au module de leur coefficient harmonique dans le plan complexe.
-
- Le son le plus simple acoustiquement parlant n'a qu'un harmonique, la fréquence fondamentale, les autres harmoniques ayant un module nul. C'est donc une sinusoïde, mais sa phase dépend de la répartition entre la partie réelle (cosinus) et imaginaire (sinus) de l'harmonique, autrement dit de son argument complexe.
Article lié : Série de Fourier
Musique
Caractéristique physique du son
Un son est une onde caractérisée physiquement par sa fréquence de vibration; elle se mesure en Hertz (en nombre de vibrations par seconde). Par exemple le "La4" (ou A4) possède une fréquence de 440 Hz. Plus un son est aigu plus sa fréquence est élevée.
Les harmoniques
La musique, intimement liée à la notion de consonance, s'est élaborée au cours du temps à partir de la décomposition d'un son en harmoniques. Une onde sonore de hauteur constante est composée d'une superposition de sons élémentaires nommés harmoniques dont les fréquences sont des multiples entiers de la fréquence fondamentale ƒ0 (2 ƒ0,3 'ƒ0,..., 6 ƒ0, 7 ƒ0, ...). Le son produit par un instrument à vent contient de nombreuses harmoniques naturelles, alors que certains instruments comme les percussions émettent des fréquences inharmoniques (2,576 ƒ0, 5,404 ƒ0, ... par exemple pour un triangle). On dit du son de ces instruments qu'ils ne contiennent que des partiels. Le spectre harmonique révèle ainsi l'ensemble des fréquences qui déterminent le timbre de chaque instrument.
Chaque harmonique possède une intensité relative par rapport aux autres. C'est le rapport d'amplitude entre ses différentes harmoniques qui fait que, par exemple, un violon n'a pas le même " timbre " qu'une flûte émettant un son de même hauteur (c'est-à-dire de même fréquence fondamentale).
En fait lorsqu'on parle de fréquence fondamentale, on parle de la fréquence de la première harmonique du son considéré, qu'on désigne comme harmonique 0 ou harmonique fondamentale. En pratique, la note que l'on entend est tout simplement l'harmonique qui a la plus grande intensité et c'est souvent la plus grave. Certains sons peuvent cependant tromper l'oreille, une harmonique aiguë pouvant s'entendre plus que la fondamentale et la cacher.
En regardant attentivement le tableau des fréquences de notes ci-dessous, les musiciens vont trouver une correspondance entre les fréquences harmoniques d'une note et les notes qui s'accordent harmonieusement avec la fondamentale. On sait par exemple que pour la note do1, les notes constituant des intervalles naturels avec elle sont mi (la tierce), sol (la quinte), si bémol (la septième), do2 (l'octave), ré (la neuvième) etc.
Les harmoniques d'une note sont donnés par les fréquences multiples de la fondamentale. Ainsi pour un do 0 à 32,7 Hz les harmoniques sont :
| Harmonique | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence | 32,7 | 65,4 | 98,1 | 130,8 | 163.5 | 196,2 | 228,9 | 261,6 | 294,3 | 327 | 359,7 | 392,4 |
| Note | Do | Do | Sol | Do | Mi | Sol | ( Sib ) | Do | Ré | Mi | ( Fa# ) | Sol |
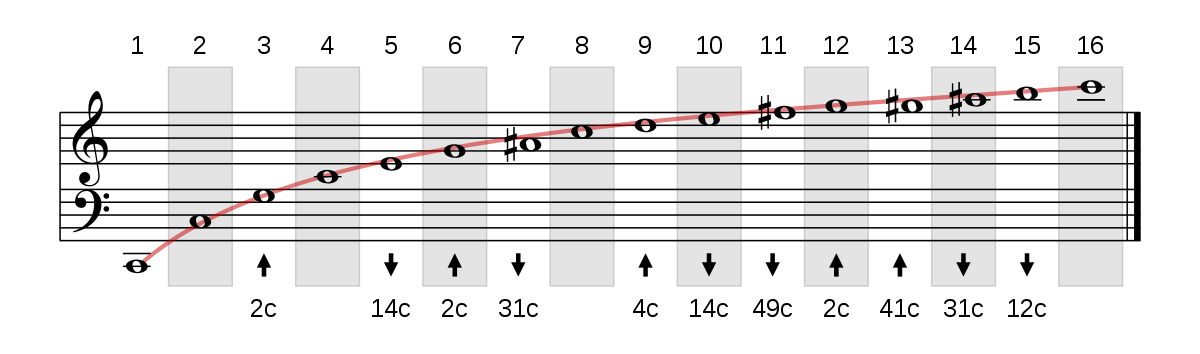
N.B. : les 7e et 11e harmoniques ne correspondent pas à des notes utilisées en musique occidentale, elles sont en dehors du cycle des quintes. Le nom indiqué est celui de la note la plus proche.
L'image ci-dessous indique les notes harmoniques d'un do grave, et précisent par les flèches et les chiffres (en cents), l'écart de hauteur entre chacune des 15 harmoniques et la note la plus proche dans le tempérament égal. Rapellons que le demi-ton (du tempérament égal) fait 100 cents ; une déviation de 49 cents est donc à mi-chemin entre deux notes existantes : c'est un quart de ton !
Quelques applications des harmoniques :
-
- Sur un piano, enfoncer doucement la pédale et faire résonner une note, permet de les écouter lorsque l'intensité sonore diminue : les cordes correspondant aux harmoniques vibrent par sympathie; la série indiquée ci-dessus est alors relativement audible.
- C'est le bon ajustement entre elles des harmoniques de deux notes entendues simultanément qui validera la consonance de l'intervalle ou de l'accord entendu. On retrouve bien les raisons pour lesquelles un accord est parfait (do-mi-sol = 4-5-6): les harmoniques des notes de l'accord sont en concordance avec les harmoniques de la fondamentale.
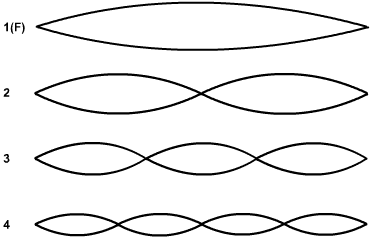
- Sur les instruments à cordes, on peut faire entendre un son harmonique en effleurant d'un doigt une division entière de la corde. Ci-dessous, les divisions correspondant à la fondamentale F (corde à vide) et aux trois premières harmoniques, et la façon de noter une note ainsi jouée.

Exemple
En prenant comme note fondamentale le "La1" (55 Hz), les harmoniques sont toutes les notes ayant pour fréquence un multiple de 55. Les harmoniques d'une note sont donc forcément plus aigu que cette note, contrairement à la théorie des harmoniques inférieures qui fut un temps avancée. Harmoniques du La1 55 Hz : 110 Hz (55x2) (La2), 165 Hz (55x3) (Mi3), 220 Hz (55x4) (La3), 275 Hz (55x5) (Do#4), 330 Hz (55x6) (Mi4), 385 Hz (55x7) (Sol4), 440 Hz (55x8) (La4), 495 Hz (55x9) (Si4)...