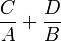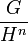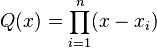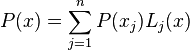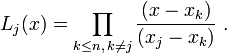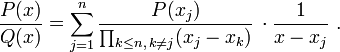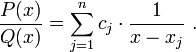Décomposition en éléments simples - Définition

Utilisations

La décomposition en éléments simples d'une fraction rationnelle a pour motivation essentielle le calcul des primitives de la fonction rationnelle correspondante sur un intervalle de ne contenant aucun pôle.

En effet, on ne sait pas en général intégrer une fonction rationnelle quelconque sur un intervalle donné.

En revanche, il existe des méthodes pour intégrer les éléments simples.

Par exemple, pour intégrer la fraction rationnelle , il suffit de la décomposer sous la forme , et en intégrant directement la somme on obtient .

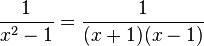
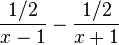
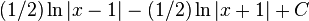
Principes généraux

Existence d'une décomposition dans tout corps

Le principe de base est assez simple ; c'est plutôt le côté algorithmique qui réclamera de l'attention dans les cas particuliers.

Soit F une fraction rationnelle sur un corps K (par exemple les nombres réels ou les nombres complexes), dont le dénominateur Q admet une factorisation Q=AB avec A et B polynômes premiers entre eux. Alors F peut s'écrire

pour certains polynômes C et D sur K. L'existence d'un telle décomposition est une conséquence du fait que l'anneau des polynômes sur K est un anneau euclidien dans lequel l'égalité

AU + BV = 1

a lieu pour certains polynômes U et V. On obtient ce dernier résultat par l'identité de Bézout.

L'utilisation de ce principe permet d'écrire F comme une somme de fractions rationnelles dont chacune a pour dénominateur une puissance d'un polynôme irréductible.

Enfin une fraction de la forme

peut s'écrire comme une somme de fractions dont le dénominateur est une puissance de H et dont les numérateurs sont de degrés inférieurs à H, plus éventuellement un autre polynôme. Ceci peut être réalisé grâce à une succession de divisions euclidiennes par H (la méthode est analogue à celle utilisée pour écrire un nombre en base a). Quand K est le corps des nombres complexes, le polynôme irréductible H est de degré 1 (théorème fondamental de l'algèbre) et les numérateurs sont donc constants. Quand K est le corps des nombres réels, le degré de H sera 1 ou 2 et les numérateurs seront linéaires ou constants.

Cas d'un dénominateur à pôles d'ordre un

Les exemples précédents peut être généralisés à la situation suivante :

Soit Q un polynôme unitaire de degré n sur un corps K dont la décomposition en facteurs de premiers degrés est

où tous les x_i sont des éléments de K différents deux à deux. En d'autres mots, Q a des racines simples sur K. Si P est un polynôme quelconque de degré , par la formule d'interpolation de Lagrange P peut être écrit de manière unique comme une somme

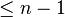
où est le j-ième polynôme de Lagrange associé à  :

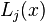
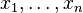
En divisant la représentation de Lagrange terme à terme par Q dans sa forme factorisée on obtient

D'où l'on déduit la décomposition en éléments simples