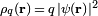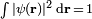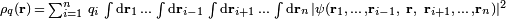Densité de charge - Définition

Densité de charge en physique quantique

Cas d'une particule

En mécanique quantique, la densité de charge correspondant à un porteur de charge est reliée à sa fonction d'onde par :

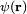
avec une fonction d'onde normalisée à l'unité par

Cas de n particules

Dans le cas de particules, la fonction d'onde dépend de l'ensemble des positions de toutes les particules, et comprend en particulier en général des corrélations, qui empêchent d'appliquer simplement la formule précédente.

Il faut exprimer la contribution de chacune des particules, de charge , en faisant la moyenne sur les positions de toutes les autres particules, puis faire la somme de ces contributions :

Une fois obtenue la distribution de charge, les considérations similaires à celles données pour le cas de la physique classique permettent de relier la densité de charge au champ électrique classique.

Si l'on veut un formalisme quantique complet, l'expression par des fonctions d'onde n'est pas suffisante : il faut les remplacer par des opérateurs, ainsi alors que le champ électrique.