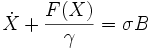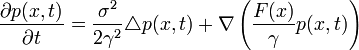Équation de Fokker-Planck - Définition

Cas du mouvement brownien

Dans le cas d'un mouvement d'une particule et dans le cadre de l'équation de Smoluchowski qui concerne les particules telles que , typiquement des molécules, ou objets de masse "négligeable" (molécules atmosphériques, protéines en biologie...) :

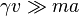
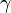
où B est un bruit blanc, le coefficient de viscosité et F(x) un champ de forces. Si p(x,t) est la probabilité de trouver la particule au point x à l'instant t, par application du lemme d'Itô on a alors :

où le coefficient de diffusion.

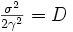
Cette équation de Fokker-Planck particulière permet alors, avec des conditions aux bords et à l'origine adéquates, d'étudier le mouvement brownien d'une particule dans un champ de forces.