Bruit blanc - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un bruit blanc est une réalisation d'un processus aléatoire dans lequel la densité spectrale de puissance est la même pour toutes les fréquences.
On parle souvent de bruit blanc gaussien, il s'agit d'un bruit blanc qui suit une loi normale de moyenne et variance données.
En synthèse et traitement du son, on ne considère que les fréquences comprises entre 20 Hz et 20 kHz puisque l'oreille humaine n'est sensible qu'à cette bande de fréquences (la sensibilité varie toutefois selon les personnes). L'impression obtenue est celle d'un souffle. Le son produit lors de l'effet de « neige » sur un téléviseur déréglé est un bon exemple de bruit blanc.

Bruit blanc sonore
Le bruit blanc, à l'instar de la lumière blanche qui est un mélange de toutes les couleurs, est composé de toutes les fréquences, chaque fréquence ayant la même énergie. Le nombre de fréquences doublant d'une octave à l'autre, l'énergie croît linéairement de 3 dB par octave.
Bruit blanc et solutions analytiques d'équations différentielles
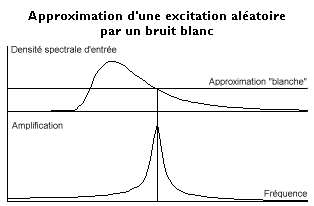
En toute rigueur un bruit blanc ne peut exister car une densité spectrale identique pour toutes les fréquences conduirait à une variance, mesurée par l'aire sous la courbe, infinie (et donc une puissance infinie).
Cette solution est néanmoins intéressante dans certains problèmes pratiques car, bien qu'il ne puisse exister, on montre que la réponse à un bruit blanc d'un système amorti reste finie. Le remplacement d'une excitation quelconque par un bruit blanc fournit donc, en simplifiant considérablement les calculs, une approximation d'autant meilleure que l'amortissement du système est plus faible.
Notion de bruit blanc
Par analogie avec la lumière blanche qui contient toutes les fréquences lumineuses avec la même intensité, un bruit blanc est un processus stochastique qui possède la même densité spectrale de puissance à toutes les fréquences. Ceci correspond à une autocorrélation nulle en tout point sauf à l'origine : le processus est décorrélé. S'il est gaussien, cette décorrélation entraîne l'indépendance.
La décorrélation conduit à une puissance moyenne ou variance infinie. Le processus correspondant ne peut donc exister mais c'est une approximation commode pour le calcul de la réponse d'un système peu amorti.
Plus concrètement, un bruit blanc filtré à la fréquence fc correspond à un processus échantillonné à 1 / 2fc, ce résultat étant utilisé dans les simulations.
Bruit blanc et statistique
Dans l'étude des séries temporelles en statistique, il est souvent utile de définir un processus de bruit blanc également dans le domaine temporel (alors que les définitions plus haut sont dans le domaine des fréquences). Les définitions présentées ici sont faites pour des processus à temps discret et à valeurs continues. Selon Hamilton (1994, p 47) :
Définition — Un processus εt est qualifié de bruit blanc si :
Un processus de bruit blanc est donc par définition stationnaire de second ordre. La troisième condition, E[εtετ] = 0, (ou
![\text{Cov}[\epsilon_t, \, \epsilon_{\tau}] = 0](https://static.techno-science.net/illustration/Definitions/autres/9/9c92d3ec7ab218314fd7dfd304ab239a_584aad944885824d9b1d662b8c9bc502.png)
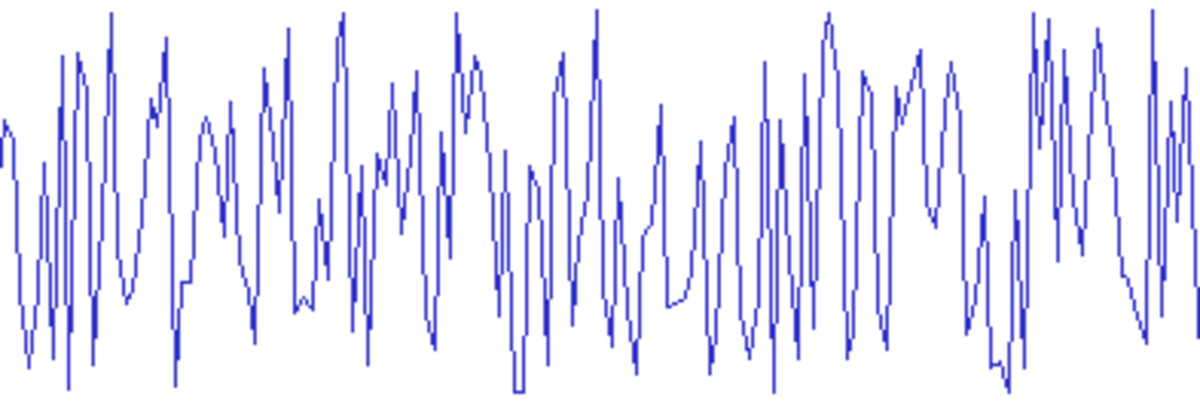
Définition — Un processus εt est qualifié de bruit blanc indépendant si :
-
-
-
-
-
-
-
-
![E[\epsilon_t]=0 \,](https://static.techno-science.net/illustration/Definitions/autres/d/d4e9df0014121bcca20184a0188f732b_cb14e8b62bf787a5dd332a67ce294968.png)
-
![E[\epsilon_{t}^{2}]=\sigma ^2](https://static.techno-science.net/illustration/Definitions/autres/2/20221ad1d41ec8556e6c318485d2174a_032b7d23c5020c2dcd8cc388d3df10ed.png)
-
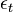
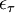
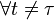
-
-
-
-
-
-
-
On remarquera que la troisième condition de la définition du bruit blanc indépendant, celle d'indépendance, implique la condition d'autocovariance nulle du bruit blanc, tandis que la réciproque n'est pas forcément vraie. Cette deuxième définition est donc plus stricte que la première.
Définition — Un processus εt est qualifié de bruit blanc gaussien si
-
-
-
-
-
-
-
- εt est un bruit blanc indépendant
-
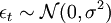
-
-
-
-
-
-
![E[\epsilon_t \epsilon_{\tau}]=0 \qquad \forall t \ne \tau](https://static.techno-science.net/illustration/Definitions/autres/a/ab3cf5cd33877279a93003b6c1ce5f20_7404fe0a073fc801bd8523d13d0b6345.png)

















































