Équation de Schrödinger - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Naissance de l'équation - Résolution de l'équation - Formulation moderne - Bibliographie - Généralisation

Formulation moderne

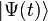
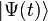
En mécanique quantique, l'état à l'instant t d'un système est décrit par un élément $\left| \Psi (t)\right\rangle$ de l'espace complexe de Hilbert — est utilisée la notation bra-ket de Paul Dirac. $\left| \Psi (t)\right\rangle$ représente les probabilités de résultats de toutes les mesures possibles d'un système.

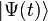
L'évolution temporelle de $\left| \Psi (t)\right\rangle$ est décrite par l'équation de Schrödinger :

où

$i$ est l'unité imaginaire ;
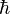
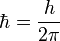
$\hbar\,$ est la constante de Planck réduite : $\hbar=\frac{h}{2\pi}$ ;
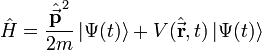
$\hat{H}=\frac{\hat{\vec{\mathbf{p}}}^2}{2m}\left| \Psi (t)\right\rangle + V(\hat{\vec{\mathbf{r}}},t)\left| \Psi (t) \right\rangle$ est l'hamiltonien, dépendant du temps en général, l'observable correspondant à l'énergie totale du système ;
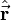
$\hat{\vec{\mathbf{r}}}\,$ est l'observable position ;
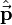
$\hat{\vec{\mathbf{p}}}\,$ est l'observable impulsion.

Contrairement aux équations de Maxwell gérant l'évolution des ondes électromagnétiques, l'équation de Schrödinger est non relativiste. Cette équation est un postulat. Elle a été supposée correcte après que Davisson et Germer eurent confirmé expérimentalement l'hypothèse de Louis de Broglie.

Bibliographie

Erwin Schrödinger ; Mémoires sur la mécanique ondulatoire, Félix-Alcan (Paris-1933). Réédition Jacques Gabay (1988), ISBN 2-87647-048-9. Contient la traduction française par Alexandre Proca des mémoires historiques de 1926 :
- Quantification et valeurs propres (I) et (II), Annalen der Physik (4) 79 (1926) ;
- Sur les rapports qui existent entre la mécanique quantique de Heisenberg-Born-Jordan et la mienne, Annalen der Physik (4) 79 (1926) ;
- Quantification et valeurs propres (III) - Théorie des perturbations avec application à l'effet Stark des raies de Balmer, Annalen der Physik (4) 80 (1926) ;
- Quantification et valeurs propres (IV), Annalen der Physik (4) 81 (1926) ; ainsi que les articles suivants :
- Le passage continu de la micro-mécanique à la mécanique macroscopique, Die Naturwissenschaften, 14 Jahrg., Heft 28 (1926), 664-666 ;
- Sur l'effet Compton, Annalen der Physik (4) 82(1927) ;
- Le théorème de la conservation d'énergie et de quantité de mouvement pour les ondes matérielles, Annalen der Physik (4) 82 (1927) ;
- Échanges d'énergie d'après la mécanique ondulatoire, Annalen der Physik (4) 83 (1927).

Préface de Marcel Brillouin. Avant-propos de l'Auteur et notes inédites spécialement écrites pour cette traduction.

(en) Erwin Schrödinger, « An Undulatory Theory of the Mechanics of Atoms and Molecules », dans Phys. Rev., vol. 28, n^o 6, décembre 1926, p. 1049-1070 .

Généralisation

La généralisation de l'équation au domaine relativiste mena à l'équation de Klein-Gordon, puis à l'équation de Dirac ; cette dernière établit naturellement l'existence du spin et des antiparticules. Cependant, il n'existe aucune interprétation entièrement cohérente de ces équations d'ondes relativistes dans le cadre d'une théorie décrivant une seule particule ; le cadre pertinent pour le théorique quantique relativiste est la théorie quantique des champs.

Il existe d'autres équations de type Schrödinger, non-linéaires, comme l'Équation de Schrödinger semi-linéaire, qui interviennent en théorie des plasmas, des lasers, etc ...