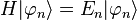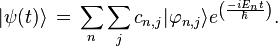Équation de Schrödinger - Définition

Résolution de l'équation

L'équation de Schrödinger étant une équation vectorielle on peut la réécrire de façon équivalente dans une base particulière de l'espace des états. Si on choisit par exemple la base correspondant à la représentation de position définie par

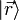
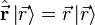
alors la fonction d'onde satisfait à l'équation suivante

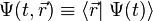
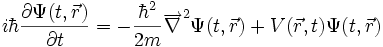
où est le laplacien. En effet l'observable position ne dépend pas du temps, donc ses états propres n'en dépendent pas non plus : .

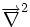
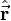
Sous cette forme on voit que l'équation de Schrödinger est une équation aux dérivées partielles faisant intervenir des opérateurs linéaires, ce qui permet d'écrire la solution générique comme la somme des solutions particulières. L'équation est dans la grande majorité des cas trop compliquée pour admettre une solution analytique de sorte que sa résolution est approchée et/ou numérique.

Recherche des états propres

Les opérateurs apparaissant dans l'équation de Schrödinger sont des opérateurs linéaires ; il s'ensuit que toute combinaison linéaire de solutions est solution de l'équation. Cela mène à favoriser la recherche de solutions qui ont un grand intérêt théorique et pratique : à savoir les états qui sont propres de l'opérateur hamiltonien.

Ces états sont donc solutions de l'équation aux états et valeurs propres,

qui porte parfois le nom d’équation de Schrödinger indépendante du temps. L'état propre est associé à la valeur propre E_n , scalaire réel, énergie de la particule dont est l'état.

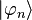
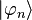
Les valeurs de l'énergie peuvent être discrètes comme les solutions liées d'un puits de potentiel (par ex. niveaux de l'atome d'hydrogène) ; il en résulte une quantification des niveaux d'énergie. Elles peuvent aussi correspondre à un spectre continu comme les solutions libres d'un puits de potentiel (par ex. un électron ayant assez d'énergie pour s'éloigner à l'infini du noyau de l'atome d'hydrogène).

Il arrive souvent que plusieurs états correspondent à une même valeur de l'énergie : l'on parle alors de niveaux d'énergie dégénérés.

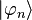
D'une façon générale, la détermination de chacun des états propres de l'hamiltonien, , et de l'énergie associée, fournit l'état stationnaire correspondant, solution de l'équation de Schrödinger :

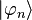
Une solution de l'équation de Schrödinger peut alors s'écrire très généralement comme une combinaison linéaire de tels états :

Selon les postulats de la mécanique quantique,

• le scalaire complexe c_n,i est l'amplitude de l'état sur l'état  ;
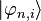
• le réel Σ_i | c_n,i | ² est la probabilité (dans le cas d'un spectre discret) de trouver l'énergie E_n lors d'une mesure de l'énergie sur le système.

Rareté d'une résolution analytique exacte

La recherche des états propres de l'hamiltonien est en général complexe. Même le cas analytiquement soluble de l'atome d'hydrogène ne l'est rigoureusement sous forme simple que si l'on néglige le couplage avec le champ électromagnétique qui va permettre le passage des états excités, solutions de l'équation de Schrödinger de l'atome, vers le fondamental.

Certains modèles simples, bien que non tout à fait conformes à la réalité, peuvent être résolus analytiquement et s'avèrent très utiles :

• particule libre (potentiel nul) ;
• oscillateur harmonique (potentiel quadratique) ;
• particule se déplaçant sur un anneau ;
• particule dans un puits de potentiel rectangulaire ;
• particule dans un guide d'onde annulaire ;
• particule dans un potentiel à symétrie sphérique ;
• particule dans un réseau unidimensionnel (potentiel périodique).

Dans les autres cas, il faut faire appel aux diverses techniques d'approximation :

• la théorie des perturbations fournit des expressions analytiques sous la forme de développements asymptotiques autour d'un problème non perturbé exactement soluble.
• l'analyse numérique permet d'explorer des situations inaccessibles par la théorie de perturbation.