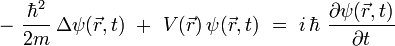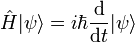Équation de Schrödinger - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Mécanique quantique | ||||||||||||||
| | ||||||||||||||
| Postulats de la mécanique quantique Histoire de la mécanique quantique
| ||||||||||||||
L'équation de Schrödinger, conçue par le physicien autrichien Erwin Schrödinger en 1925, est une équation fondamentale en physique quantique non-relativiste. Elle décrit l'évolution dans le temps d'une particule massive non-relativiste, et remplit ainsi le même rôle que la relation fondamentale de la dynamique en mécanique classique.
Naissance de l'équation
Contexte historique
Au début du XXe siècle, il était devenu clair que la lumière présente une dualité onde-corpuscule, c'est-à-dire qu'elle pouvait se manifester, selon les circonstances, soit comme une particule, le photon, soit comme une onde électromagnétique. Louis de Broglie proposa de généraliser cette dualité à toutes les particules connues bien que cette hypothèse eût pour conséquence paradoxale la production d'interférences par les électrons- à l'instar de la lumière- ce qui fut vérifié ultérieurement par l'expérience de Davisson-Germer. Par analogie avec le photon, Louis de Broglie associa ainsi à chaque particule libre d'énergie E et de quantité de mouvement p une fréquence ν et une longueur d'onde λ :
-
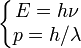
L'équation de Schrödinger, trouvée par le physicien Erwin Schrödinger en 1925, est une fonction d'onde qui généralise l'approche de de Broglie ci-dessus aux particules massives non-relativistes soumises à une force dérivant d'une énergie potentielle, dont l'énergie mécanique totale est classiquement :
-
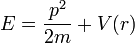
Le succès de l'équation, déduite de cette extension par utilisation du principe de correspondance, fut immédiat quant à l'évaluation des niveaux quantifiés d'énergie de l'électron dans l'atome d'hydrogène, car elle permit d'expliquer les raies d'émission de l'hydrogène : séries de Lyman, Balmer, Brackett, Paschen, etc.
L'interprétation physique correcte de la fonction d'onde de Schrödinger ne fut donnée qu'en 1926 par Max Born. En raison du caractère probabiliste qu'elle introduisait, la mécanique ondulatoire de Schrödinger suscita initialement de la méfiance chez quelques physiciens de renom comme Albert Einstein, pour qui « Dieu ne joue pas aux dés ».
La dérivation historique
Le schéma conceptuel utilisé par Schrödinger pour dériver son équation repose sur une analogie formelle entre l'optique et la mécanique :
- En optique ondulatoire, l'équation de propagation dans un milieu transparent d'indice réel n variant lentement à l'échelle de la longueur d'onde conduit - lorsqu'on cherche une solution monochromatique dont l'amplitude varie très lentement devant la phase - à une équation approchée dite de l'eikonale. C'est l'approximation de l'optique géométrique, à laquelle est associé le principe variationnel de Fermat.
- Dans la formulation hamiltonienne de la mécanique classique, il existe une équation dite de Hamilton-Jacobi. Pour une particule massive non relativiste soumise à une force dérivant d'une énergie potentielle, l'énergie mécanique totale est constante et l'équation de Hamilton-Jacobi pour la "fonction caractéristique de Hamilton" ressemble alors formellement à l'équation de l'eikonale (le principe variationnel associé étant le principe de moindre action.)
Ce parallèle avait été noté dès 1834 par Hamilton, mais celui-ci n'avait alors pas de raison de douter de la validité de la mécanique classique. Après l'hypothèse de De Broglie de 1923, Schrödinger s'est dit : l'équation de l'eikonale étant une approximation de l'équation d'onde de l'optique ondulatoire, cherchons l'équation d'onde de la "mécanique ondulatoire" (à construire) dont l'approximation soit l'équation de Hamilton-Jacobi. Ce qu'il a fait, d'abord pour une onde stationnaire (E = cte), puis pour une onde quelconque.
Remarque : Schrödinger avait en fait commencé par traiter le cas d'une particule relativiste - comme d'ailleurs de Broglie avant lui. Il a alors obtenu l'équation connue aujourd'hui sous le nom de Klein-Gordon, mais son application au cas du potentiel coulombien donnant des niveaux d'énergie incompatibles avec les résultats expérimentaux de l'atome d'hydrogène, il se serait rabattu sur le cas non-relativiste, avec le succès que l'on connaît.
Une fois établi le parallèle entre l'optique et la mécanique hamiltonienne - i.e. la partie non-triviale du raisonnement -, la fin de la dérivation est relativement élémentaire. En effet, l'équation d'onde satisfaite par l'amplitude spatiale d'une onde monochromatique de pulsation ω fixée dans un milieu d'indice n lentement variable s'écrit :
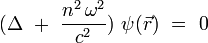
On introduit le nombre d'onde k dans le milieu d'indice n, tel que :
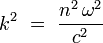
On obtient alors l'équation de Helmholtz :
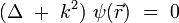
La longueur d'onde dans le milieu est définie par :λ = 2π / k. L'équation de Helmholtz se réécrit :
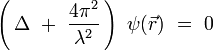
On utilise alors la relation de de Broglie pour une particule non-relativiste, pour laquelle la quantité de mouvement p = m v :
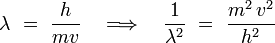
Or, l'énergie cinétique s'écrit pour une particule non-relativiste :
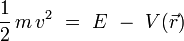
d'où l'équation de Schrödinger stationnaire :
![\left[ \, \Delta \ + \ \frac{8\pi^2m}{h^2} \, \left( \, E \ - \ V(\vec{r}) \, \right) \ \right] \ \psi(\vec{r}) \ = \ 0](https://static.techno-science.net/illustration/Definitions/autres/8/8c7d80fc7d1da2d83269927bd383f764_5b51109030e2f13ed4d8b48f8046f8e3.png)
En introduisant le quantum d'action
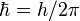
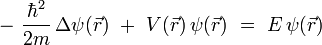
Il ne reste plus qu'à réintroduire le temps t en explicitant la dépendance temporelle pour une onde monochromatique, puis en utilisant la relation de Planck-Einstein
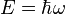
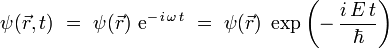
On obtient finalement l'équation de Schrödinger générale :