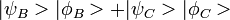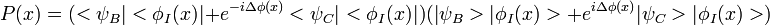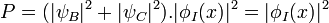Expérience de la gomme quantique à choix retardé - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Description de l'expérience - Enjeux et interprétations - Figures d'interférences - Enjeux et interprétations - complément

Enjeux et interprétations - complément

Considérons la situation où la "gomme quantique" est présente. La complémentarité des figures d'interférence obtenues par corrélation des points reçus sur l'écran I avec les signaux reçus en G et H est une donnée importante qui doit être interprétée. On nommera ces figures Fig(G) et Fig(H). On appellera de même Fig(0) la figure obtenue en absence d'interférences.

Si la figure d'interférence était identique dans les deux cas (Fig(G) = Fig(H)), l'impact d'un photon sur une frange sombre de cette figure pourrait donner une information de type probabiliste. Nous pourrions dire dans ce cas qu'il y a davantage de chance de détecter le photon en J ou K (cas où il n'y a pas interférence car on détecte quel chemin le photon a emprunté) qu'en G ou H (cas où il y a interférence car la détection en G ou H n'apporte pas d'information sur le chemin emprunté).

Mais ce n'est pas le cas : les figures d'interférence sont exactement complémentaires (Fig(G)+Fig(H)=Fig(0)). Si le photon tombe sur une frange sombre de Fig(G) alors cela donne bien une information de type probabiliste : si le photon est détecté en G ou H alors le photon a davantage de chance d'être détecté en H (probabilité d'être détecté en H sachant qu'il est détecté en G ou en H). Mais cette information n'a aucun lien avec la connaissance du chemin emprunté par le photon.

Mathématiquement, la fonction d'onde juste après les convertisseurs bas s'écrit :

$\displaystyle |\psi_B>|\phi_B>+|\psi_C>|\phi_C>$

On a noté $ψ$ la fonction d'onde d'un photon signal et $φ$ celle d'un photon témoin. Juste avant l'impact sur l'écran I, on a :

$\displaystyle (|\psi_B>|\phi_I(x)>+e^{i\Delta \phi(x)}|\psi_C>|\phi_I(x)>)$

La probabilité d'impact en un point x de l'écran est :

$\displaystyle P(x) = (<\psi_B|<\phi_I(x)|+e^{-i\Delta \phi(x)}<\psi_C|<\phi_I(x)|) (|\psi_B>|\phi_I(x)>+e^{i\Delta \phi(x)}|\psi_C>|\phi_I(x)>)$

Les fonctions $| ψ B >$ et $| ψ C >$ sont orthogonales donc :

Il n'y a pas d'interférence. L'observation d'un impact en un point $x 0$ réduit la fonction d'onde du photon signal à $| φ I (x 0) >$ . Il s'agit d'une constante que l'on peut éliminer dans la suite. L'espace se réduit donc à un espace à une seule particule :

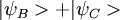
$\displaystyle |\psi_B> + |\psi_C>$

Dans l'expérience de Marlan Scully décrite un peu plus précisément dans l'article de Kim, la particule témoin prend la différence de phase de la particule signal. Comme après l'observation sur l'écran on connaît cette différence de phase, on a :

$\displaystyle |\psi_B> + e^{i \phi(x_0)}|\psi'_B>$

Comme les miroirs semi-réfléchissants introduisent des déphasages de $Π / 2$ , on a finalement au niveau des détecteurs finaux :

$\displaystyle (1 \pm e^{i \phi(x_0)})|\psi_B>$

Le signe + ou - dépend du détecteur G ou H. On observe donc la corrélation avec la première observation car la différence de phase a été "enregistrée" dans la deuxième particule. Il n'y a donc aucune transmission d'une information du futur vers le passé : la connaissance du résultat x0 de la mesure en I pour le photon signal modifie, pour l'observateur, la probabilité de détection du photon témoin en G ou en H, de telle manière qu'apparaisse une figure d'interférence. La mécanique quantique explique correctement cette expérience de façon déterministe. Il n'y aurait pas eu de corrélation si expérimentalement la particule témoin n'avait pas pris la différence de phase de la particule signal.