Forme cristalline - Définition

Classification des formes cristallines

Parmi les différents critères de classification, les suivants sont les plus importants :

Formes caractéristiques et non-caractéristiques

Ce critère intègre la possibilité de cristaux de symétries différentes de développer la même forme.

Notons G le groupe ponctuel qui correspond à la symétrie propre de la forme et H le groupe ponctuel du cristal qui a développé cette forme : soit H coïncide avec G lui-même ; soit avec un de ses sous-groupes, ce qu'on écrit H G.

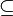
Lorsque H = G, on parle de « forme caractéristique », tandis que H G correspond à une « forme non-caractéristique ». Dans les systèmes cristallins triclinique et monoclinique, toute forme est non-caractéristique.

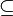
Formes générales et particulières

Lorsque les pôles des faces d'une forme cristalline se trouvent sur des éléments de symétre (axes ou miroirs), la forme est dite « particulière », sinon elle est « générale ».

Exemple 1

Le prisme ditétragonal à symétrie propre 4/mmm : il se présente comme forme {hk0} dans les groupes ponctuels 4/mmm, 42m, 4mm et 422. C'est donc seulement dans le premier cas qu'il s'agit d'une forme caractéristique.

Exemple 2

Le prisme tétragonal se présente comme forme {100} dans tous les groupes ponctuels tétragonaux. Toutefois, il s'agit d'une forme particulière dans les groupes 4/mmm, 42m, 4mm, 422 et 4/m, mais d'une forme générale dans les groupes 4 et 4.

Formes basiques et limites

Lorsqu'une forme peut être obtenue comme limite d'une autre forme ayant la même multiplicité (nombre de faces) et la même orientation mais une symétrie propre supérieure, cette forme s'appelle « forme limite » et celle à partir de laquelle cette forme a été obtenue s'appelle « forme basique ».

Exemple

Dans le groupe ponctuel 4mm la pyramide tétragonale et le prisme tétragonal ont multiplicité 4 et peuvent être orientés soit selon les axes soit selon les bissectrices des axes. La pyramide, forme basique, a symétrie propre 4mm tandis que le prisme, forme limite, a symétrie propre 4/mmm. Le prisme peut être imaginé comme le résultat de l'ouverture de la pyramide à son sommet et du changement de la pente des faces, jusqu'au limite où celles-ci deviennent parallèles, formant ainsi un prisme.

Bibliographie

• International Tables for Crystallography, Volume A, cinquième édition (2005), chapitre 10, publié par l'Union internationale de cristallographie