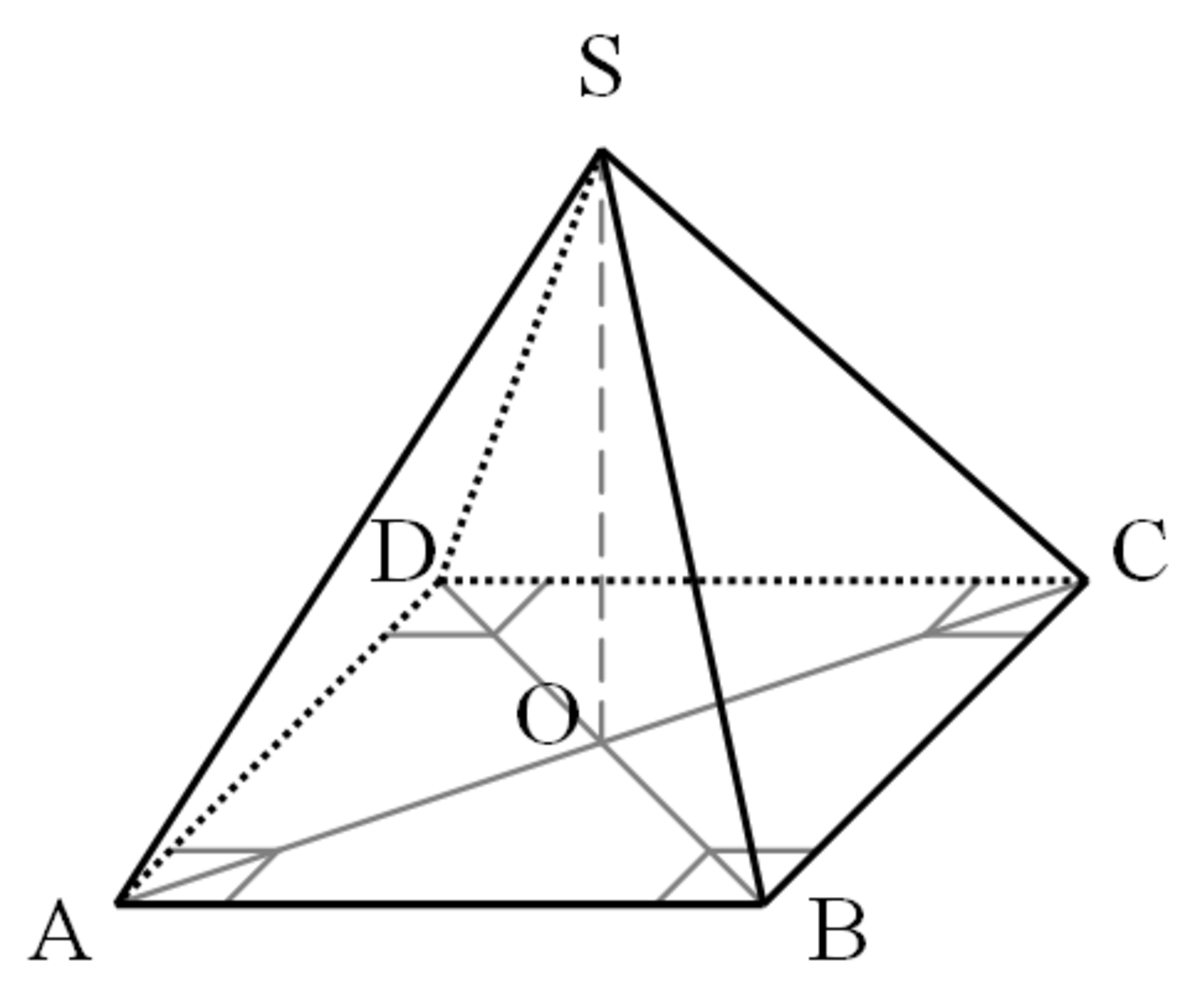
Pyramide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Ensemble des pyramides | |
|---|---|
| |
| Faces | n triangles, 1 n-gone |
| Arêtes | 2n |
| Sommets | n+1 |
| Groupe de symétrie | Cnv |
| Polyèdre dual | Auto-duaux |
| Propriétés | convexe |
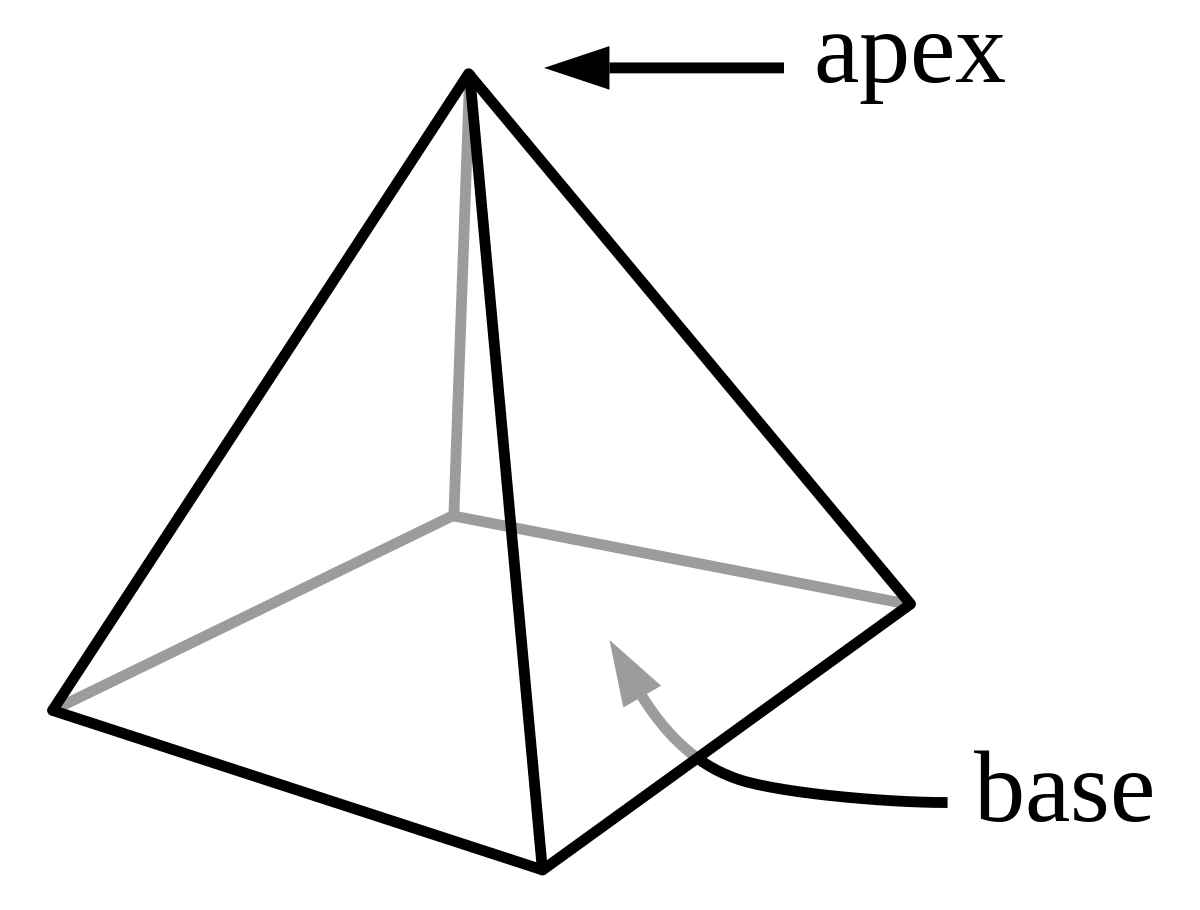
Une pyramide (du grec pyramis) à n côtés est un polyèdre formé en reliant une base polygonale de n côtés à un point, appelé l'apex, par n faces triangulaires (n ≥ 3). En d'autres mots, c'est un solide conique avec une base polygonale.
Lorsque cela n'est pas précisé, la base est supposée carrée. Pour une pyramide triangulaire chaque face peut servir de base, avec le sommet opposé pour apex. Le tétraèdre régulier, un des solides de Platon, est une pyramide triangulaire. Les pyramides carrées et pentagonales peuvent aussi être construites avec toutes les faces régulières, et par conséquent sont des solides de Johnson. Toutes les pyramides sont des auto-duaux.
Les pyramides sont une sous-classes des prismatoïdes.
Origine du nom
Ce sont les Grecs qui ont introduit le nom de « pyramide », comparant les pyramides d'Égypte avec une de leurs pâtisseries de forme similaire appelée « pyramis » ou « pyramous ».
Aire de la surface
L'aire de la surface d'une pyramide régulière, c'est-à-dire une pyramide dont toutes les faces sont des triangles isocèles identiques, est
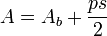
Volume
Le volume d'une pyramide est
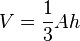
Ceci peut être démontré par le calcul suivant :
- En utilisant le fait que les dimensions d'une section plane parallèle à la base augmente de façon linéaire à partir de l'apex vers la base. Alors, la section plane à une hauteur quelconque y est la base mise à l'échelle par un facteur de
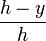
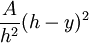
- Le volume est donné par l'intégrale
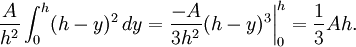
(Trivialement, le volume d'une pyramide à base carrée avec un apex d'hauteur égale à la moitié de la base peut être vue comme un sixième d'un cube formé par six pyramides de cette sorte (en paires opposées) par le centre. Alors "base fois la hauteur" correspond à un demi du volume du cube, et par conséquent trois fois le volume de la pyramide, ce qui donne le facteur un tiers).
Généralisation aux dimensions supérieures
Une pyramide est un objet géométrique ayant pour base un polygone quelconque, auquel on relie tous ses sommets à un point unique. Par abus de langage, on dit qu'elle est régulière si toutes ses faces sont des polygones réguliers.
En généralisant, une hyperpyramide de dimension 4 est un polychore ayant pour base un polyèdre auquel on relie tous ses sommets à un point unique. Le pentachore en est l'exemple le plus simple.
Et donc, une hyperpyramide de dimension n est un polytope à n dimensions, qui a pour base un polytope à n-1 dimensions, et dont tous les sommets sont reliés à un point unique. Une hyperpyramide peut être considérée comme l'ensemble de tous les "états" pris par sa base lors de son rétrécissement progressif jusqu'à l'apex le long d'une médiane centrale (reliant le centre de gravité de la base au sommet); tous ces "états" de la base sont en fait l'intersection de l'hyperpyramide avec des hyperplans parallèles à la base. L'hypervolume d'une hyperpyramide de dimension n est donné par la formule :
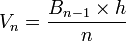
| Nom | Point | Segment | Triangle | Pyramide | 4-hyperpyramide | 5-hyperpyramide |
|---|---|---|---|---|---|---|
| Explication | rien (d=-1) n'est relié à un point (d=0) | un point (d=0) est relié à un point (d=0) | un segment (d=1) est relié à un point (d=0) | un polygone (d=2) est relié à un point (d=0) | un polyèdre (d=3) est relié à un point (d=0) | un polychore (d=4) est relié à un point (d=0) |
| Dimension | 0 | 1 | 2 | 3 | 4 | 5 |
| Image |

|
|

|
|  |
Tout simplexe est une hyperpyramide, et la plus simple de chaque dimension.