Cristallographie - Définition

Introduction

La cristallographie est la science qui se consacre à l'étude des substances cristallines à l'échelle atomique. Les propriétés physico-chimiques d'un cristal sont étroitement liées à l'arrangement spatial des atomes dans la matière. L'état cristallin est défini par un caractère périodique et ordonné à l'échelle atomique ou moléculaire. Le cristal est obtenu par translation dans toutes les directions d'une unité de base appelée maille élémentaire.

Elle est en rapport avec des disciplines aussi diverses que la physique, la chimie, les mathématiques, la biophysique, la biologie, la médecine, la science des matériaux, la métallurgie ainsi que les sciences de la terre.

Historique

Le cristal, d'abord simple objet de curiosité, passionna les collectionneurs avant d'intriguer les savants qui, en étudiant sa structure, ébauchèrent les premières théories sur la constitution intime de la matière. La loi des indices rationnels ou des troncatures simples fut définie par l'abbé René Just Haüy en 1774. Par observation du phénomène de clivage de la calcite, il a déterminé les « molécules intégrantes », c'est-à-dire les parallélépipèdes identiques constituant les cristaux et suite à cela, il a été déduit que chaque face d'un cristal peut être repérée dans l'espace par des nombres entiers.

Le cristal parfait

Le « cristal parfait » est un modèle utilisé pour représenter la structure de la matière cristalline. Ce modèle considère qu'un cristal est un empilement ordonné et infini d'atomes, d'ions ou de molécules.

Le cristal est un solide à structure constituée d'atomes ordonnés dans un réseau périodique et même tripériodique et symétrique. Il a des propriétés de symétrie avec des axes de rotation directs et inverses, des miroirs, des plans et des centres de symétrie.

Un cristal peut être isotrope (même indice de réfraction de la lumière dans toutes les directions) ou anisotrope (deux indices différents dans deux directions perpendiculaires).

La maille élémentaire est le plus petit volume cristallin conservant toutes les propriétés physiques, chimiques et géométriques du cristal. Elle est définie par trois vecteurs qui génèrent ainsi six paramètres de maille : les trois longueurs des vecteurs a, b, c et trois angles α, β, γ.

Le réseau cristallin

Un réseau est un ensemble de points ou « nœuds » en trois dimensions qui présente la propriété suivante : lorsque l'on se translate dans l‘espace selon certains vecteurs, on retrouve exactement le même environnement. Il y a donc une périodicité spatiale. Cela permet de définir sept systèmes réticulaires de base : cubique, hexagonal, rhomboédrique, quadratique (ou tétragonal), orthorhombique, monoclinique et triclinique.

Le réseau de Bravais

Le français Auguste Bravais définit, en 1848, à partir des différentes combinaisons des éléments de symétrie cristalline, 32 classes de symétrie, qui elles-mêmes se répartissent en 14 types de réseaux (il n'existe pas d'autre façon de disposer des points dans l'espace, afin de réaliser un réseau ou une maille, de manière à ne laisser aucun volume libre entre les réseaux). Les 14 réseaux de Bravais sont des expansions des 7 formes primitives de cristaux.

Voici deux exemples des réseaux de Bravais primitifs :

• Triclinique:

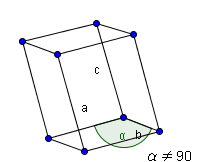
on a et aucun des angles n'est égal à 90°.

• Monoclinique:

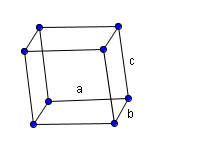
Le deuxième réseau de Bravais est le réseau monoclinique. Celui-ci est composé de 2 bases rectangulaires et de 4 côtés ayant la forme de parallélogrammes. Les trois longueurs a, b et c ne sont pas égales : , mais deux des trois angles sont à 90º.

On peut le trouver en réseau primitif (P ), ou en réseau à base centrée (C ) (un nœud au milieu de la face définie par les axes a et b).

Les indices de Miller

Haüy a défini des indices (P, Q, R) qui permettent de repérer dans l'espace les faces d'un cristal. Miller, pour simplifier, a dit qu'il ne fallait pas utiliser P, Q et R mais leurs inverses (1/P, 1/Q, 1/R) qui seront notés h, k, l. Ils doivent être entiers, premiers entre eux et de valeurs simples.

Groupes ponctuels de symétrie et groupes d'espace

Le groupe ponctuel de symétrie d'un système cristallin est le groupe (au sens mathématique) regroupant l'ensemble des opérations de symétrie qui laissent un nœud du réseau invariant. Ce nœud est donc situé à l'intersection de toutes les opérations de symétrie, dont la translation ne fait pas partie. Il existe 32 groupes ponctuels de symétrie distincts.

Le groupe d'espace d'un système cristallin regroupe l'ensemble des opérations de symétrie du groupe ponctuel, auxquelles s'ajoutent les opérations de translation. Vers 1890, Fedorov et Schoenflies démontrèrent - indépendamment l'un de l'autre - l'existence de 230 groupes, qui représentent toutes les combinaisons possibles de réseaux et d'opérations de symétrie.

Pour plus d'information, voir les articles :

• système cristallin ;
• groupe ponctuel de symétrie ;
• groupe d'espace.