Point (géométrie) - Définition
En géométrie, un point est le plus petit élément constitutif de l'espace de travail.
En géométrie euclidienne élémentaire
Le point, selon Euclide, est ce qui n'a aucune partie. On peut aussi dire plus simplement qu'un point ne désigne pas un objet mais un emplacement. Il n'a donc aucune dimension, longueur, largeur, épaisseur, volume ou aire. Sa seule caractéristique est sa position. On dit parfois qu'il est " infiniment petit ". Toutes les figures du plan et de l'espace sont constituées d'ensemble de points.
Le point étant considéré comme l'unique élément commun à deux droites sécantes, on représente habituellement le point par une croix (intersection de deux petits segments) plutôt que par un point (signe).
Lorsque le plan ou l'espace est muni d'un repère cartésien, on peut positionner tout point par rapport aux axes de ce repère par ses coordonnées cartésiennes ; le point est alors associé à un couple de réels en dimension 2 ou un triplet de réels en dimension 3. Il existe cependant d'autres manières de repérer les points (coordonnées polaires en dimension deux, coordonnées sphériques ou coordonnées cylindriques en dimension 3)
En géométrie affine
Dans un espace affine E associé à l'espace vectoriel V, les éléments de E sont appelés les points et les éléments de V sont appelés les vecteurs. À chaque couple de points (A,B), on associe un vecteur :
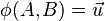
- La relation de Chasles : φ(A,B) + φ(B,C) = φ(A,C)
- Si A est fixé, il y a correspondance bijective entre les points de l'espace affine E et les vecteurs de l'espace vectoriel V, c'est l'application qui, au point B, associe le vecteurφ(A,B).
En géométrie projective
En géométrie projective, les points de l'espace projectif E associé à l'espace vectoriel V sont les droites vectorielles de V. Lorsque l'espace vectoriel V est de dimension n, et qu'il lui est associé un espace affine A, il est fréquent d'associer à l'espace E deux ensembles de points : l'ensemble des points d'un sous-espace affine A' de dimension n-1 d'équation x = 1 (par exemple) et l'ensemble des droites vectorielles du sous-espace vectoriel V' associé à A' L'espace projectif E est alors assimilé à un espace affine A' auquel on ajoute les droites vectorielles de V' . On distingue alors, dans E, les points de type affine (ceux dans A') et les autres appelés points à l'infini.
En particulier, si

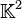

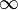
Histoire
La notion de point, en mathématiques, a aujourd'hui un sens très large. Historiquement, les points étaient les " constituants " fondamentaux, les " atomes ", dont étaient faits les droites, les plans et l'espace, tels que les concevaient les géomètres grecs de l'Antiquité. on disait ainsi qu'une droite, un plan ou l'espace tout entier étaient des ensembles de points.
Depuis la création de la théorie des ensembles par Georg Cantor à la fin du XIXe siècle et l'explosion des " structures mathématiques " qui s'en est suivie, on utilise le terme de " point " pour désigner un élément quelconque d'un ensemble que l'on décide arbitrairement d'appeler " espace " : c'est ainsi que l'on parlera d'un point de la droite des nombres réels ( alors que les Grecs faisaient évidemment la distinction entre un " point " et un " nombre " ), d'un point d'un espace métrique, d'un espace topologique, d'un espace projectif, etc.
Bref, il suffit qu'un mathématicien qualifie " d'espace " tel ou tel ensemble, au sens le plus général de ce terme et muni de propriétés particulières régies par des axiomes, pour que ses éléments soient aussitôt qualifiés de " points ".
Ainsi, aujourd'hui, le terme " d'espace " étant presque devenu synonyme " d'ensemble ", le terme " point " est donc presque devenu synonyme " d'élément ". Ces termes " d'espace " et de " points " sont juste utilisés pour leur pouvoir suggestif, même si ces termes en question n'ont plus rien à voir avec la géométrie.

















































