Forme cristalline - Définition

Introduction

Une forme cristalline est un ensemble de faces d'un cristal qui sont dans un rapport de symétrie.

Une forme cristalline est caractérisée par :

• la multiplicité qui est le nombre des faces ; elle dépend de la symétrie du cristal et de l'orientation de la face originale par rapport aux éléments de symétrie du cristal ;
• sa symétrie propre  ;
• son nom officiel. La nomenclature officielle française des formes cristallines fut publiée dans : J.D.H. Donnay et H. Curien, « Nomenclature des 47 formes cristallines » Bulletin de la Société française de Minéralogie et Cristallographie, 81 (1958) XLIV-XLVII.

Représentation des formes cristallines

On distingue deux sortes de forme cristalline :

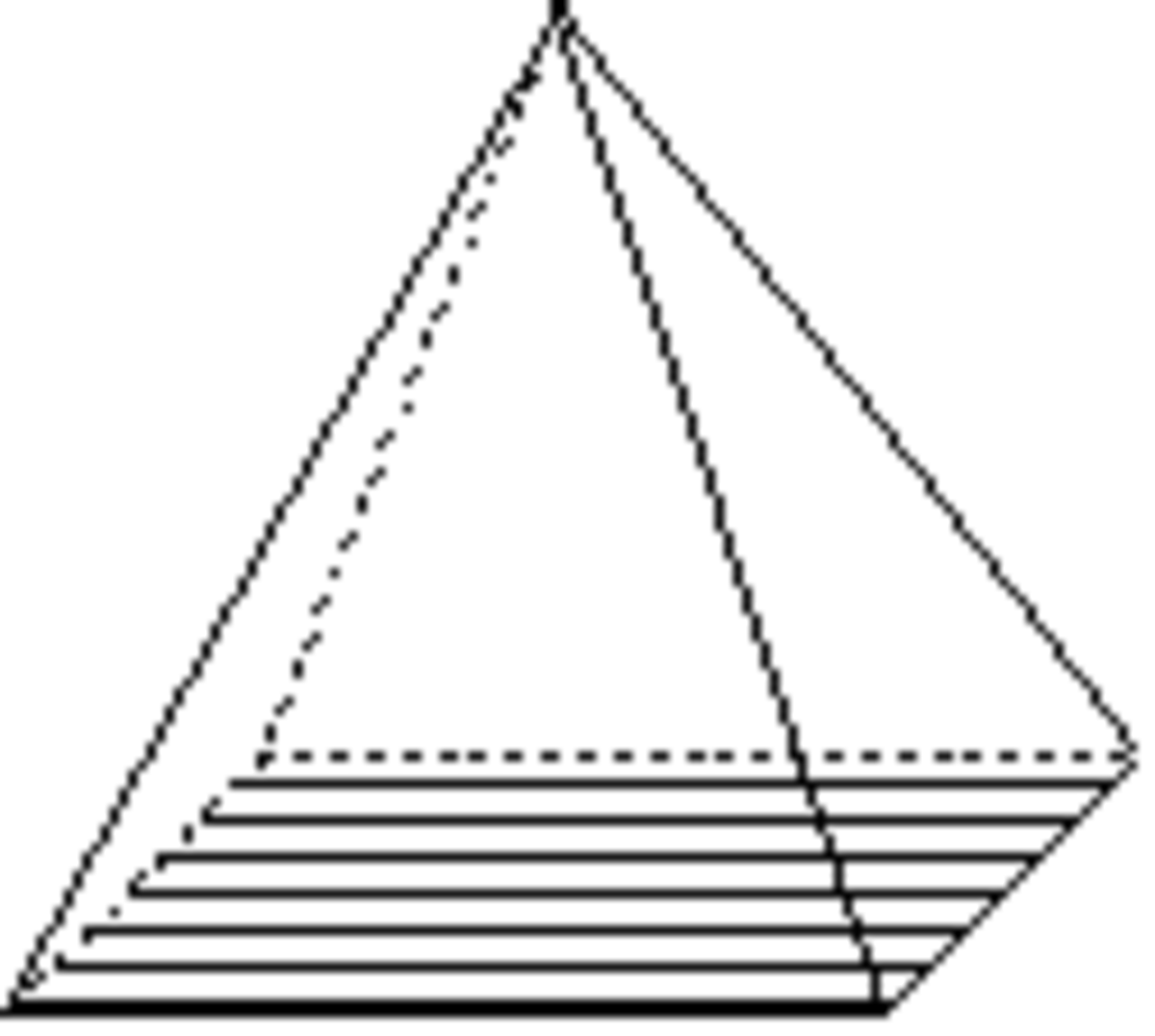
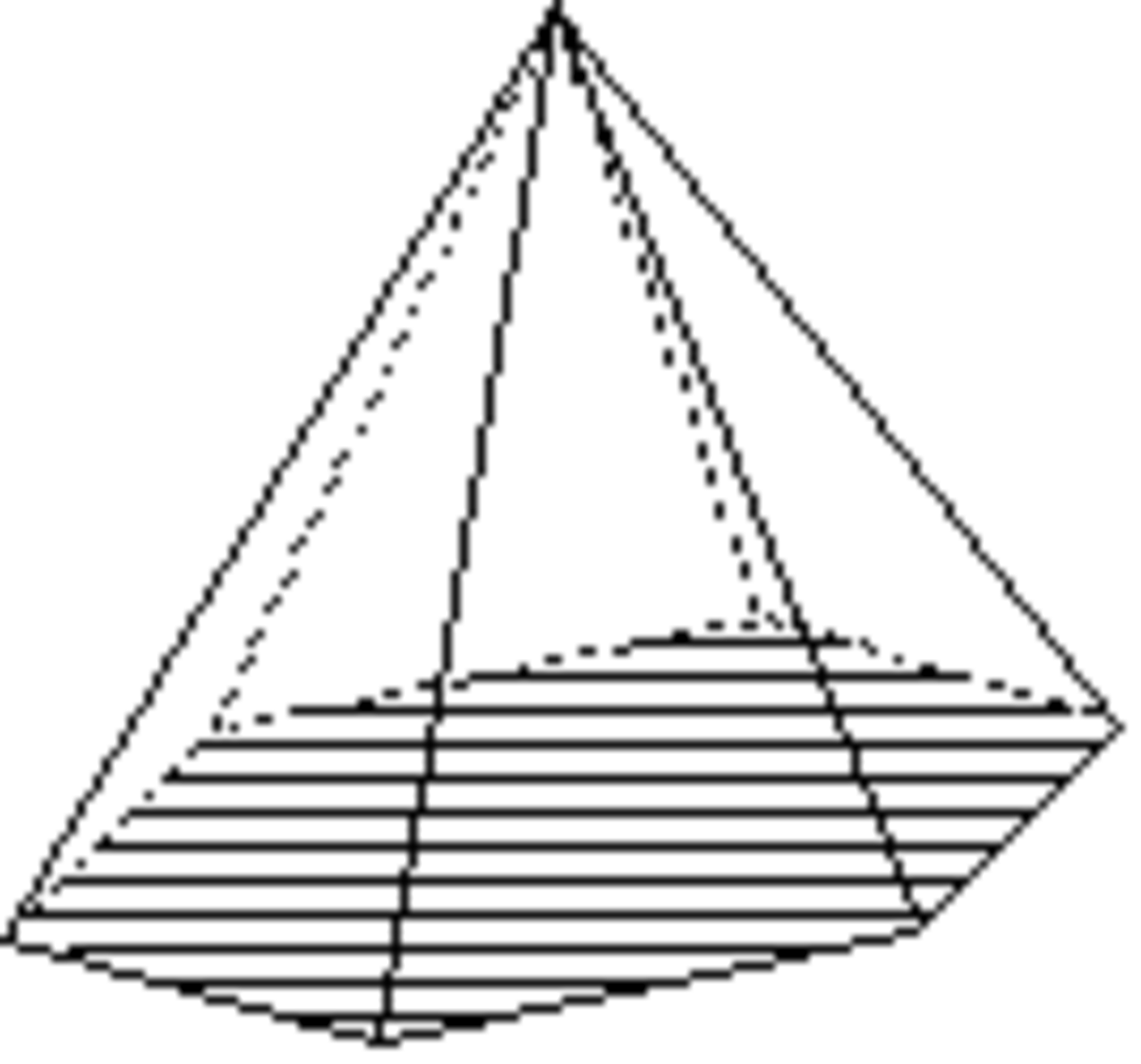
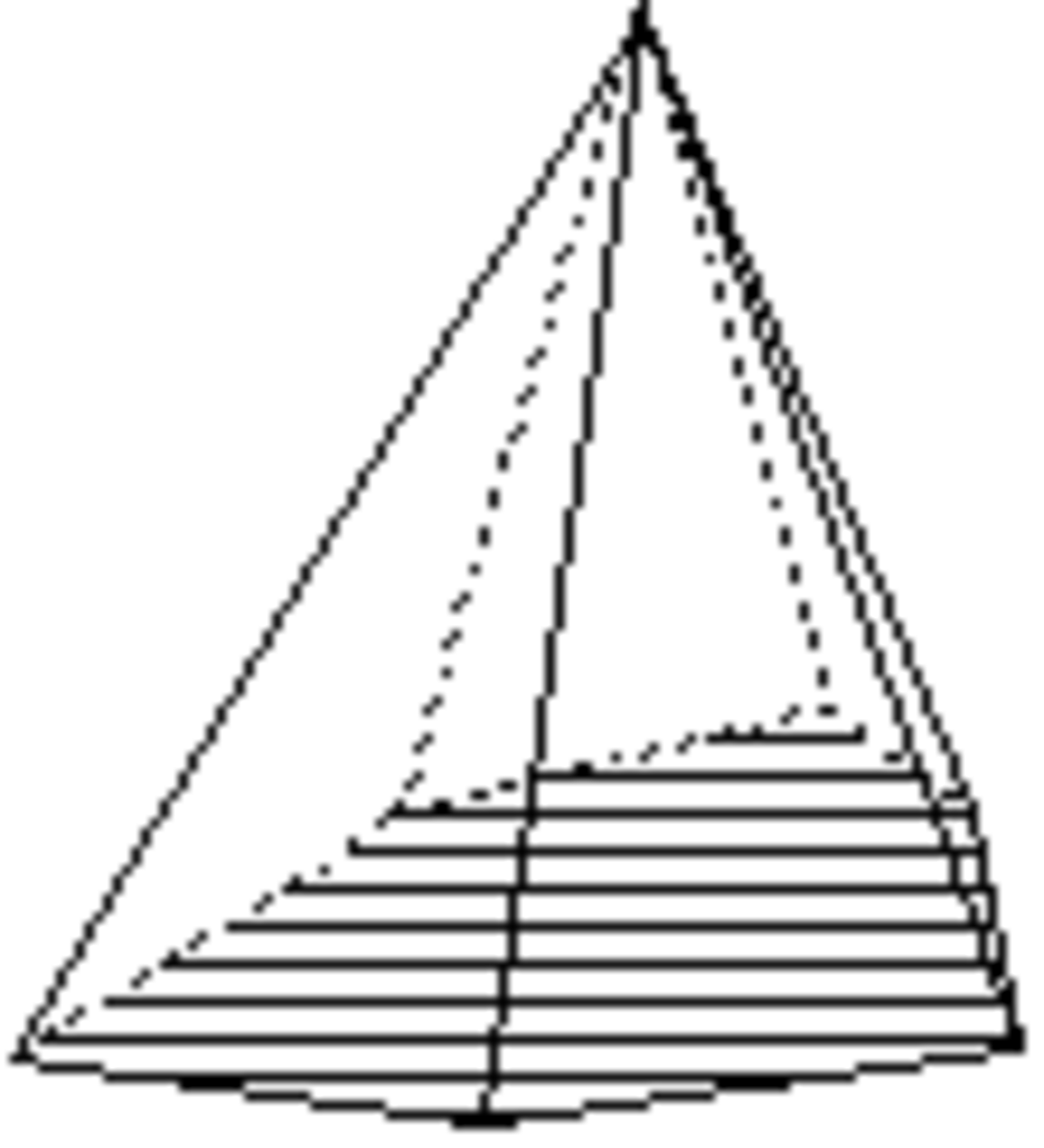
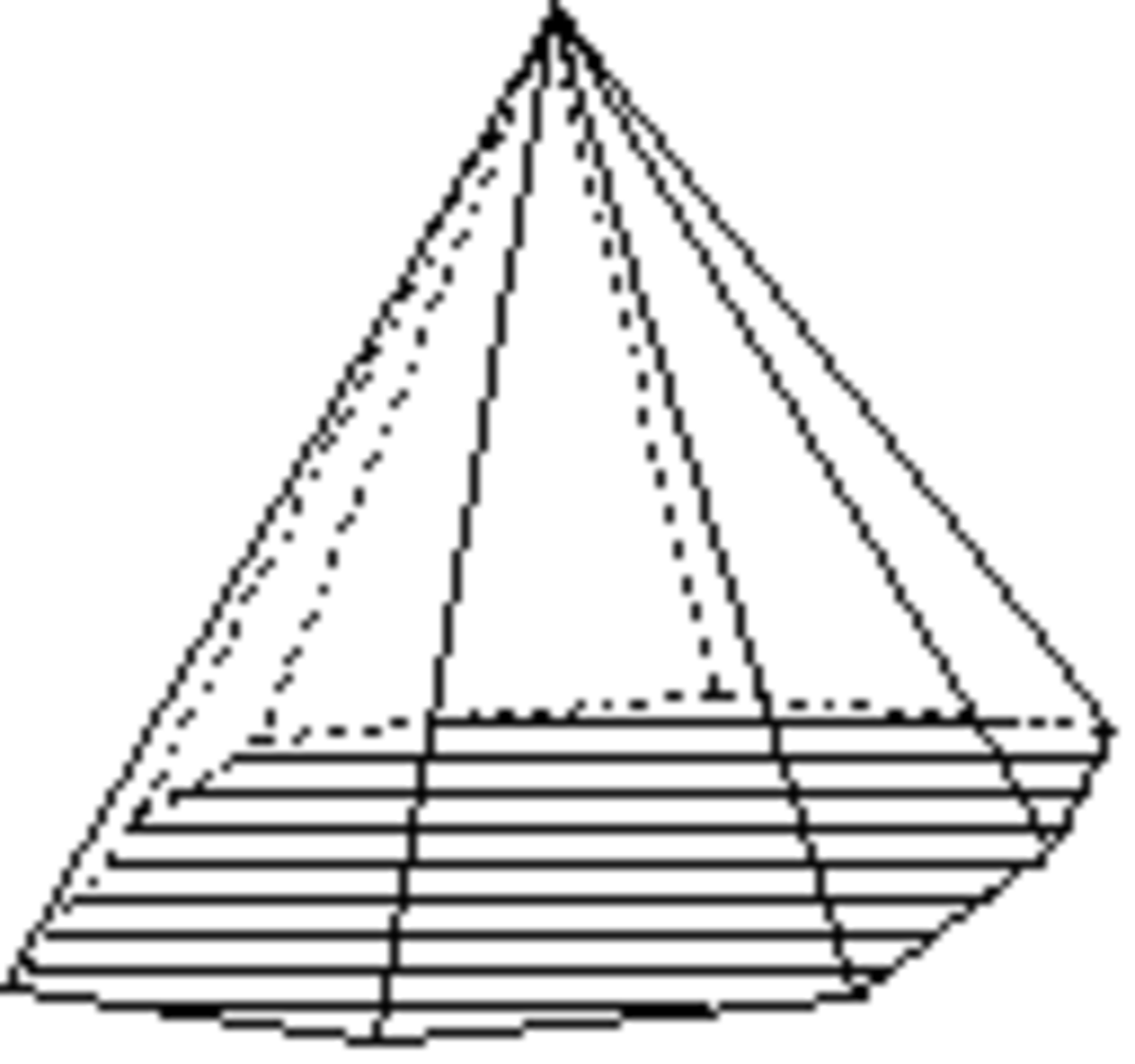
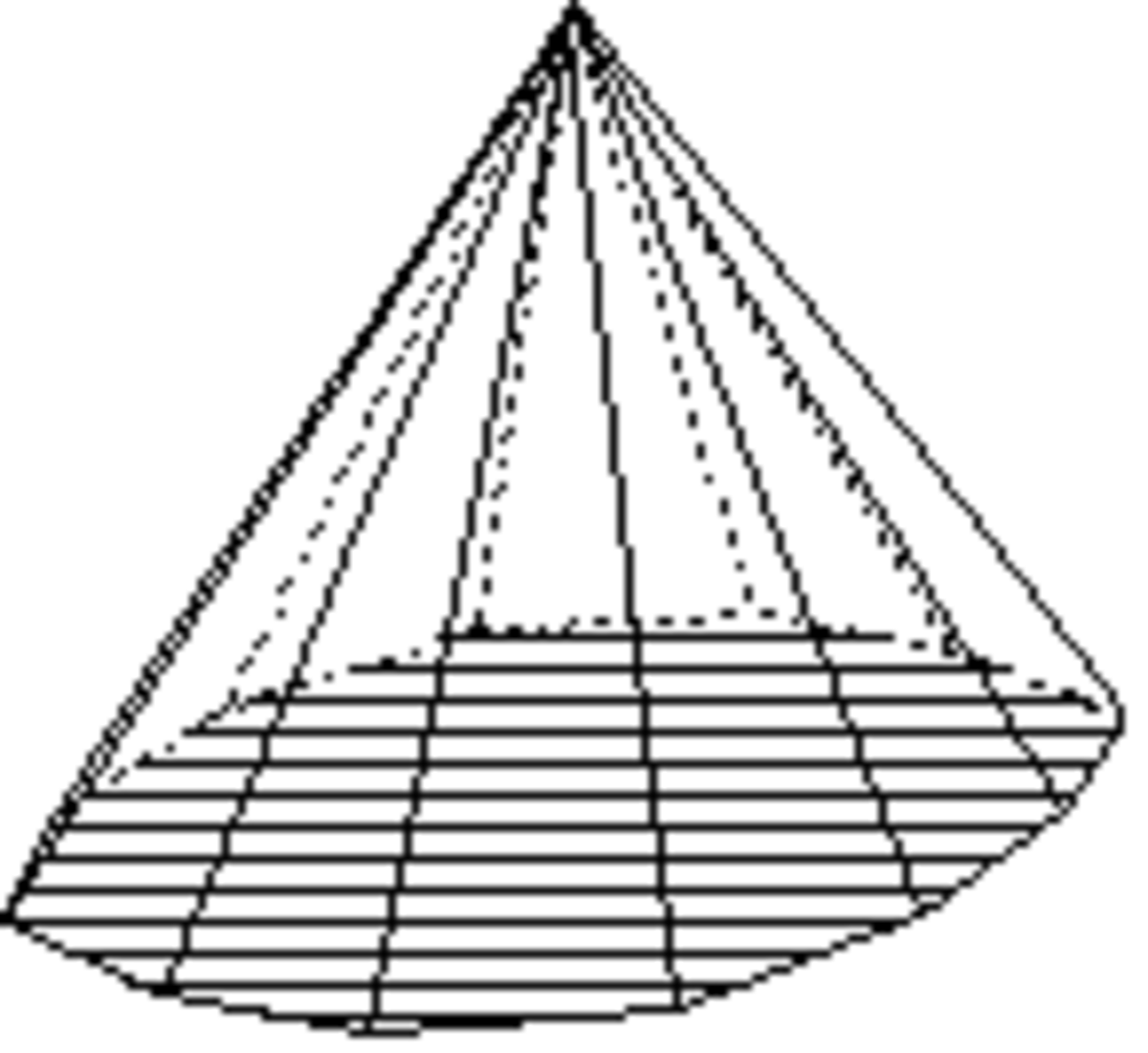
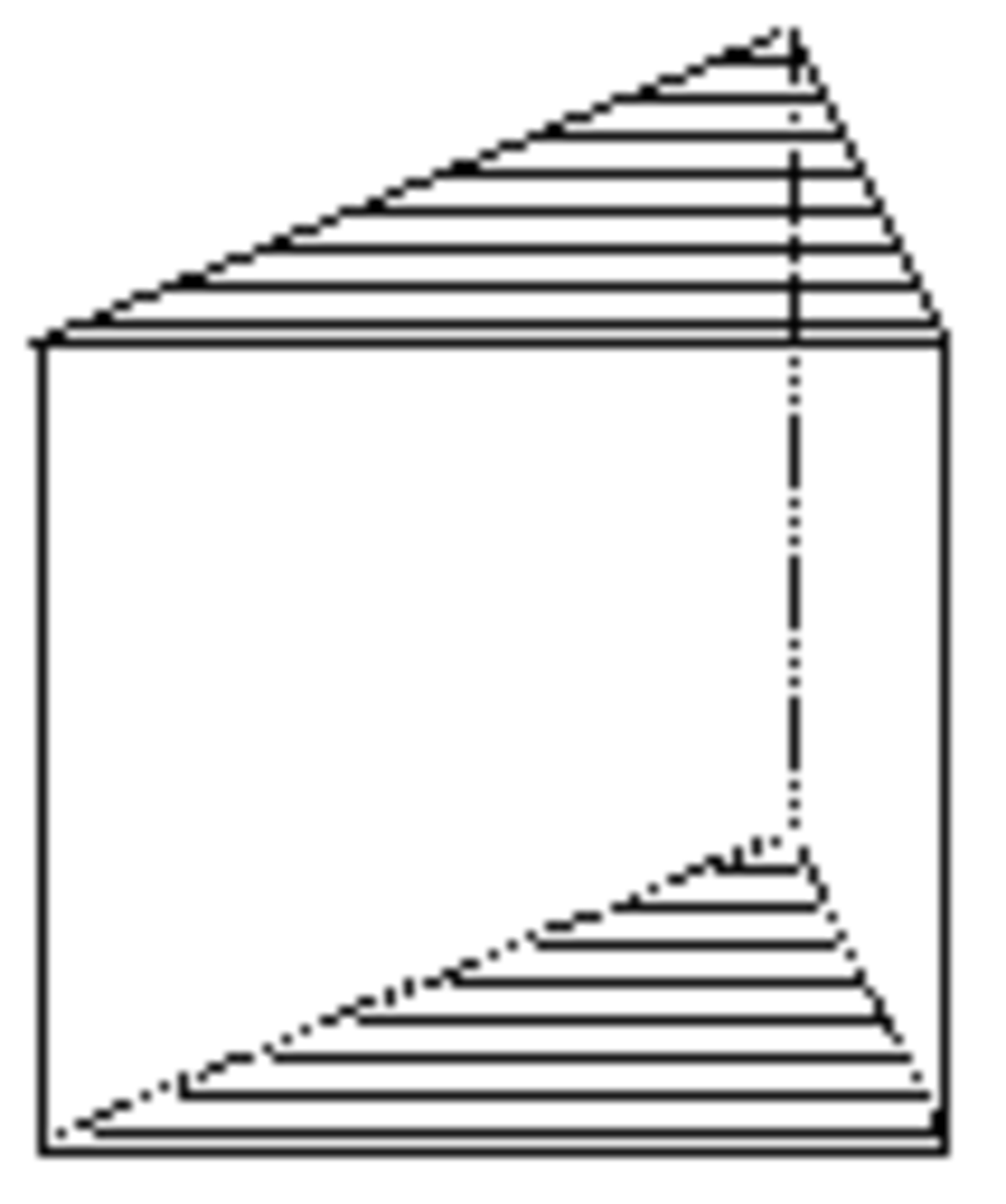
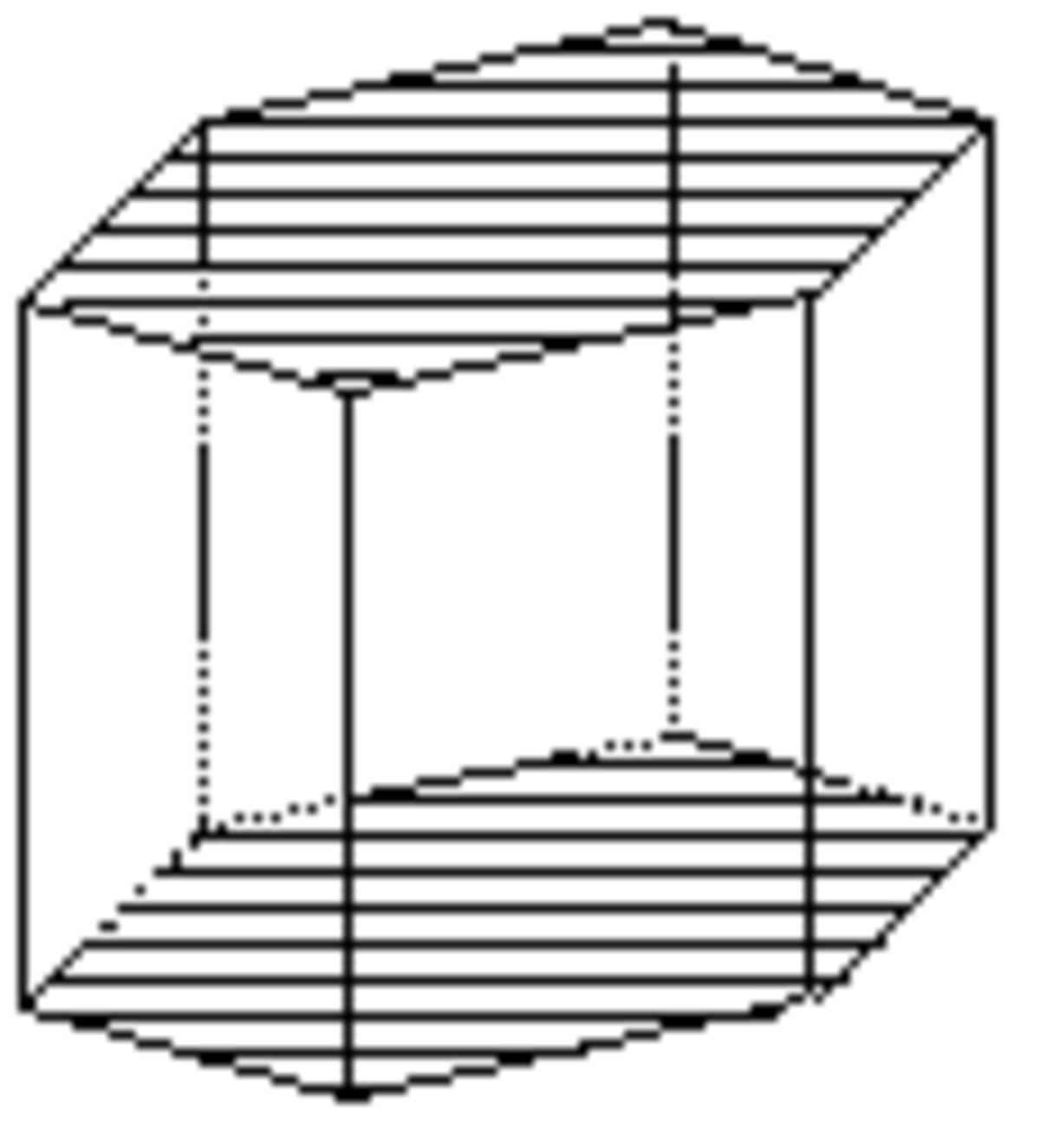
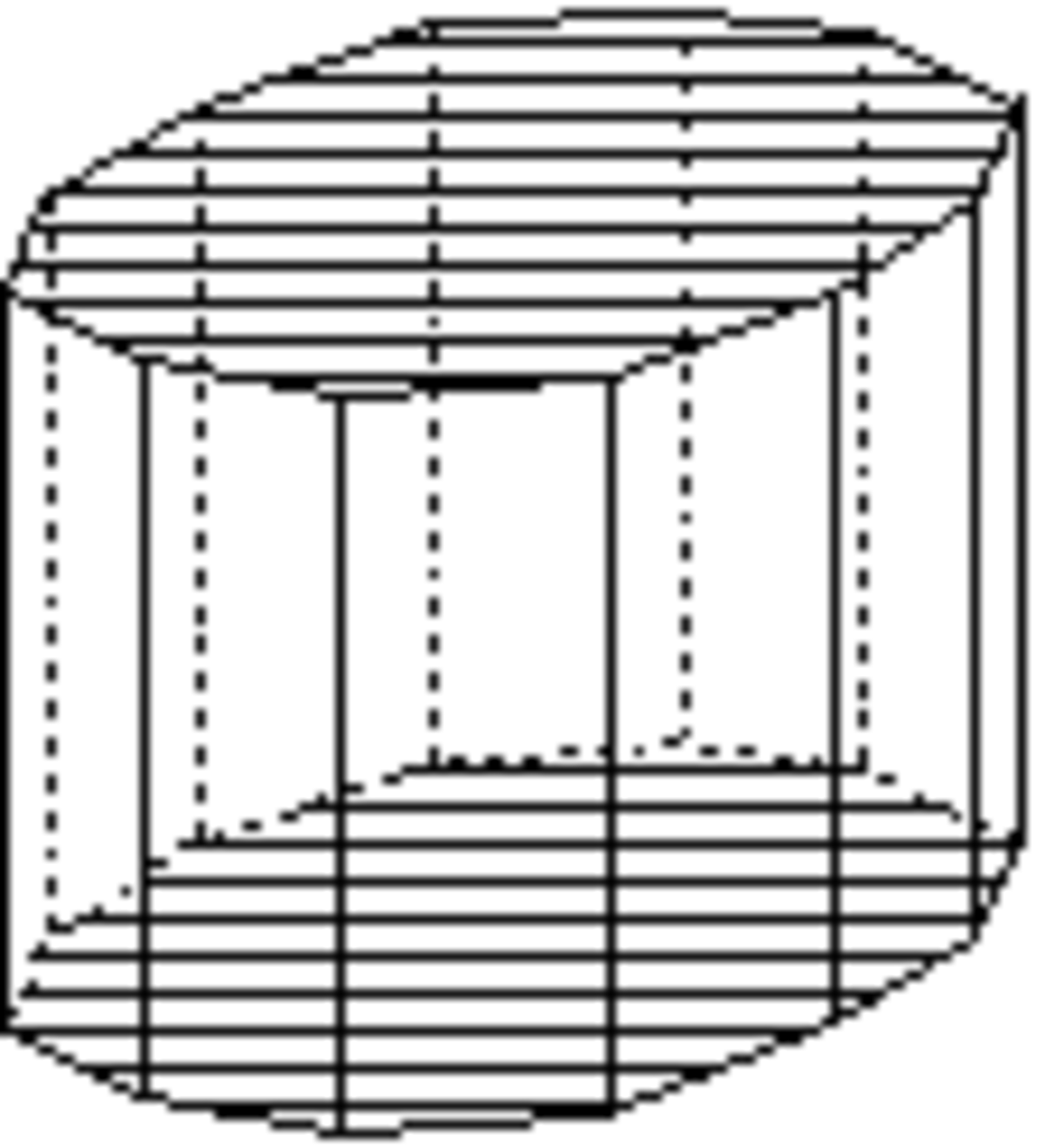
• les formes ouvertes dont les faces ne forment pas rigoureusement un volume ; une ou plusieurs faces du volume n'appartenant pas à la forme cristalline. Dans les représentations graphiques, on reconnaît ces formes à l'absence d'une ou plusieurs faces ; absence qui peut être figurée par exemple à l'aide de polygones hachés comme ci-dessous ;
• les formes fermées qui sont des volumes, aucune face ne manquant.

Un cristal ne peut donc pas consister en une seule forme ouverte, tandis qu'il peut développer une seule forme fermée.

Une forme est indiquée par les indices d'une de ses faces, de préférence celle qui a les valeurs les plus positives. Les indices d'une forme sont écrits entre accolades.

Exemple

La forme {111} comprend la face (111) et toutes les faces équivalentes à (111) par symétrie.

• Si le groupe ponctuel du cristal est 1, la forme {111} a multiplicité 2 et est composée de deux plans parallèles, (111) et (1 1 1) : cette forme s'appelle pinacoïde.
• Si le groupe ponctuel du cristal est 3, la forme {111} a multiplicité 8 et est composée de huit faces qui sont des triangles équilatères : (111), (111), (111), (111), (11 1), (111), (1 11) et (1 1 1). Cette forme est un octaèdre.

Les 47 formes cristallines

Les formes ouvertes sont ci-dessous montrées avec des polygones hachés ou grisés pour indiquer le ou les plans non fermés.

Pedion

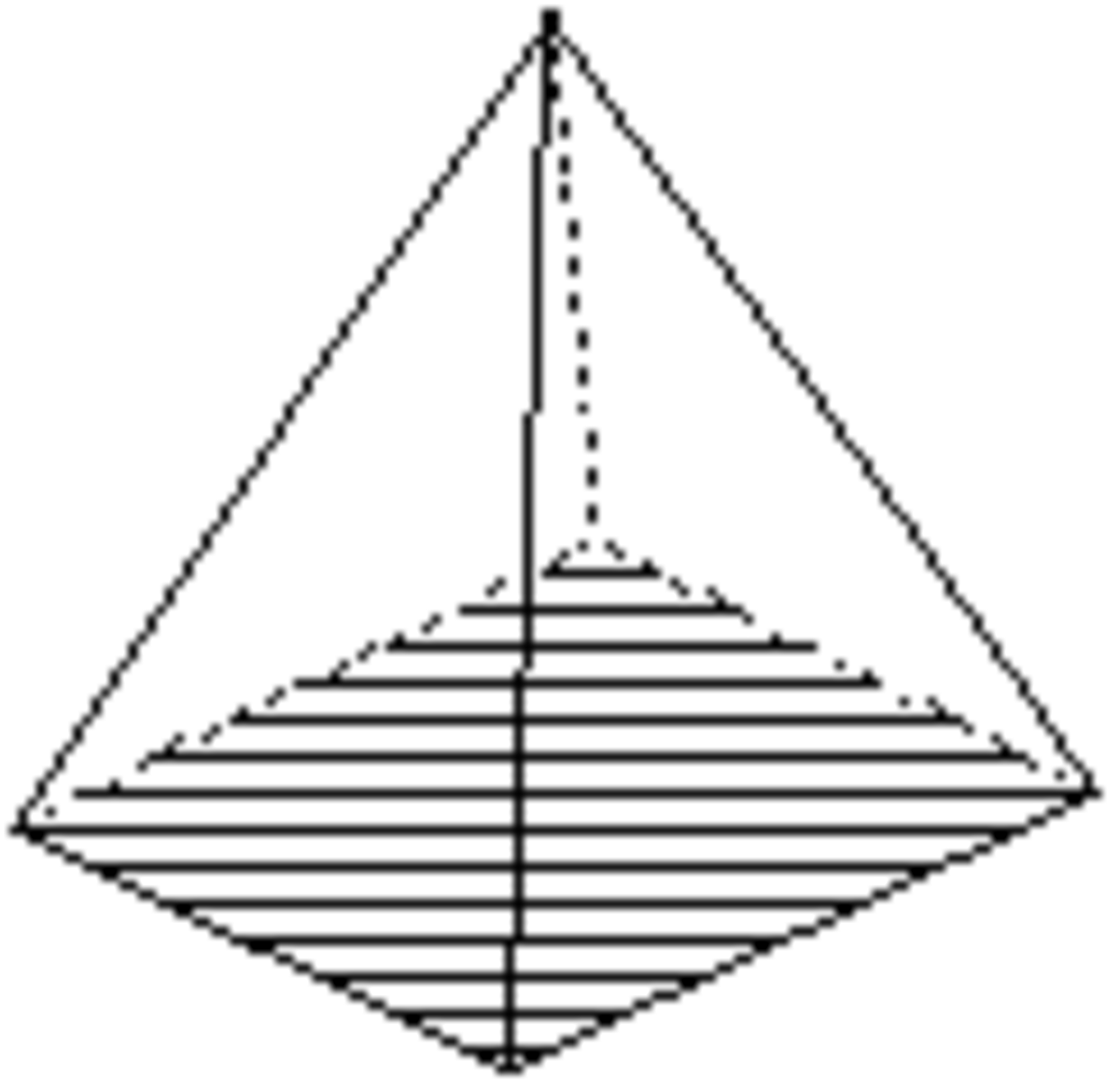
Pedion

Dite aussi monoèdre, cette forme ouverte est composée d'un seul plan. Sa symétrie propre est m.

Pinacoïde

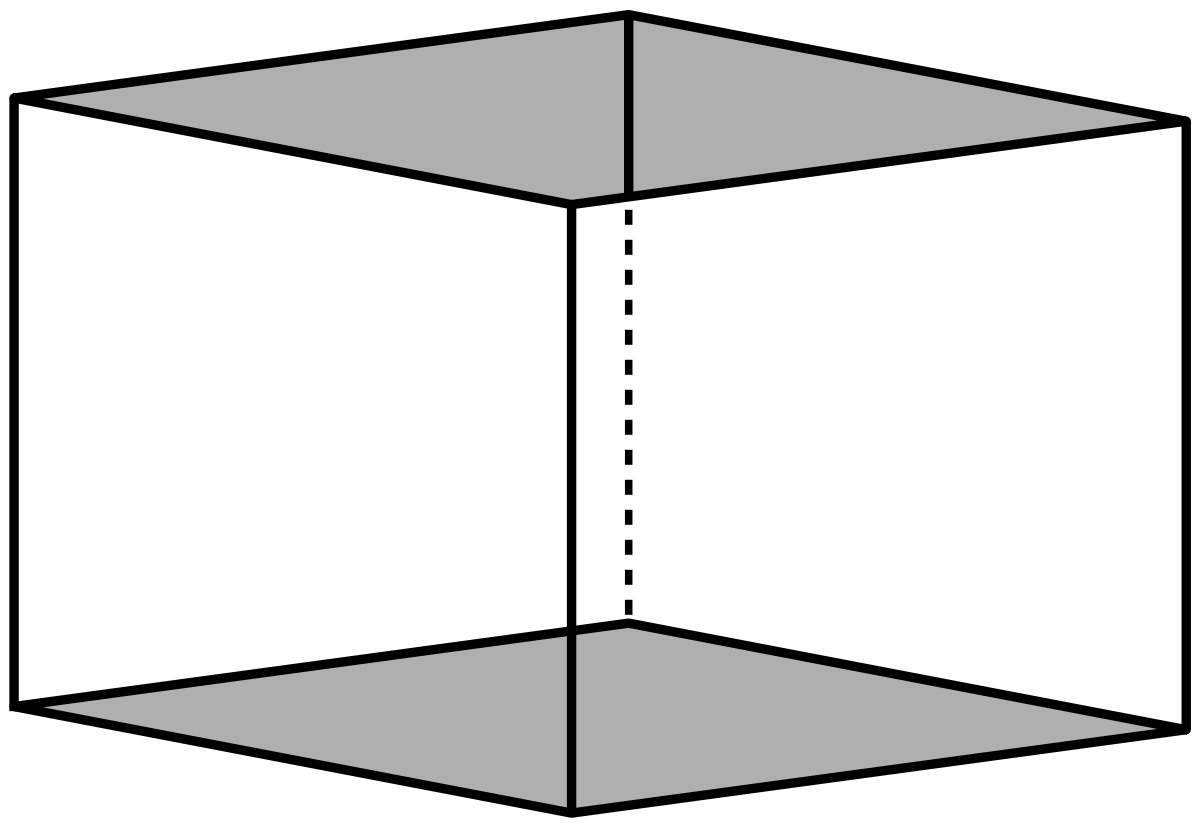
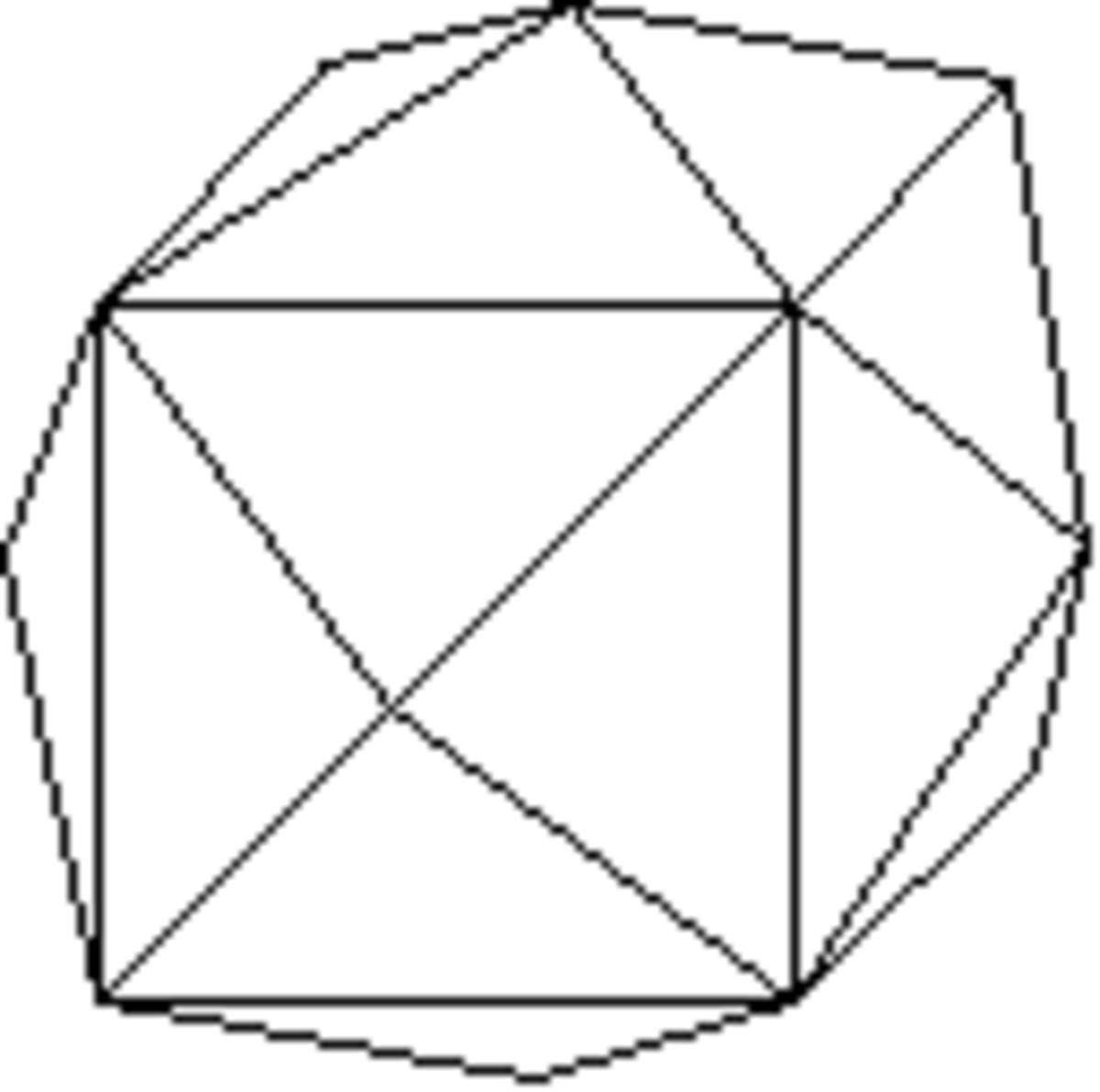
Pinacoïde

Forme ouverte composée de deux plans parallèles. Sa symétrie propre est m/m.

Dièdre

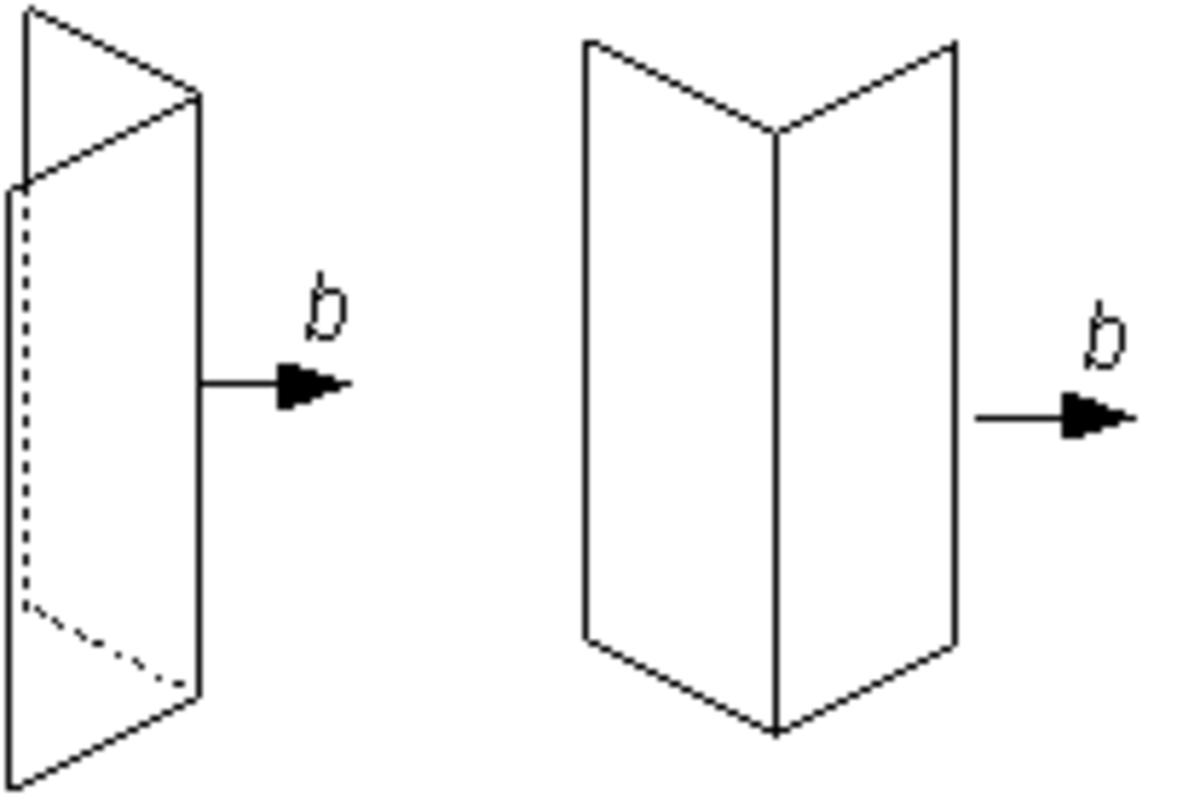
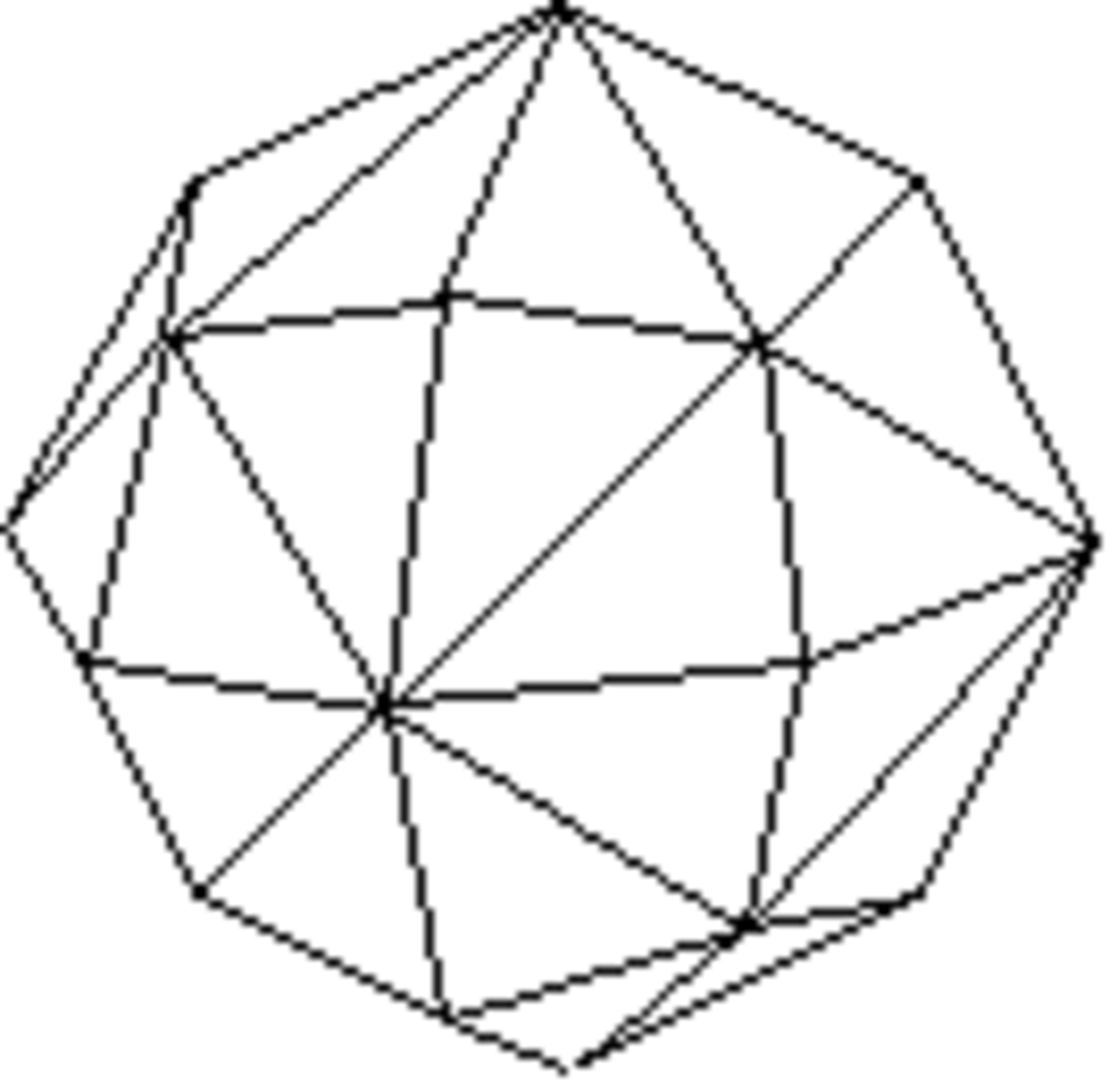
Dièdre

Forme ouverte composée de deux plans qui se coupent en une arête commune. Sa symétrie propre est mm2.
Les deux plans peuvent être reliés par un axe binaire ou par un miroir ; le dièdre prend respectivement le nom de sphénoïde ou de dome. La distinction entre sphénoïde et dome porte à 48 le nombre de formes cristallines.

Prisme rhombique

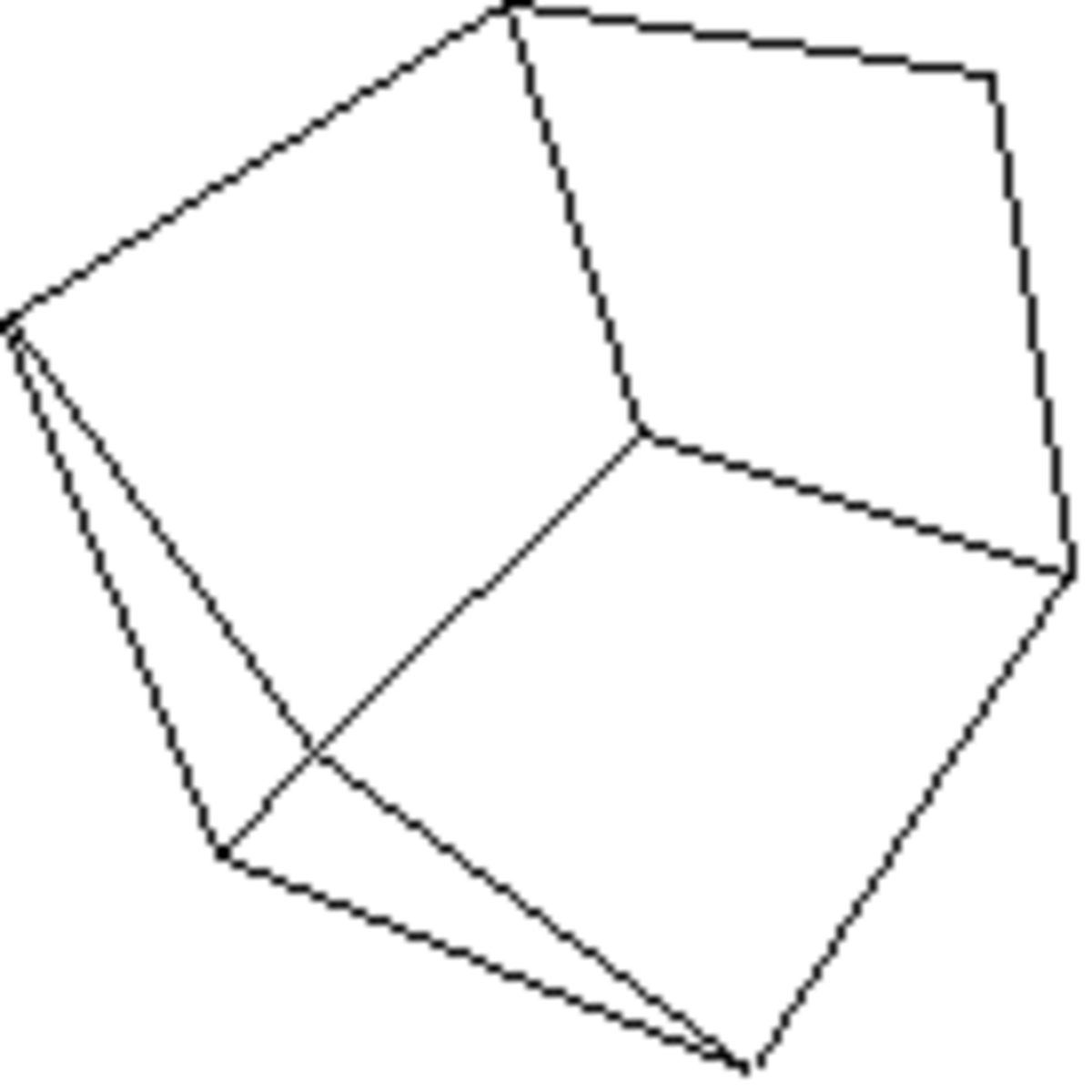
Prisme rhombique

Forme ouverte composée de quatre plans non parallèles. Sa symétrie propre est mmm.

Pyramide rhombique

Pyramide rhombique

Forme ouverte composée de quatre triangles scalènes. Sa symétrie propre est mm2.

Pyramide trigonale

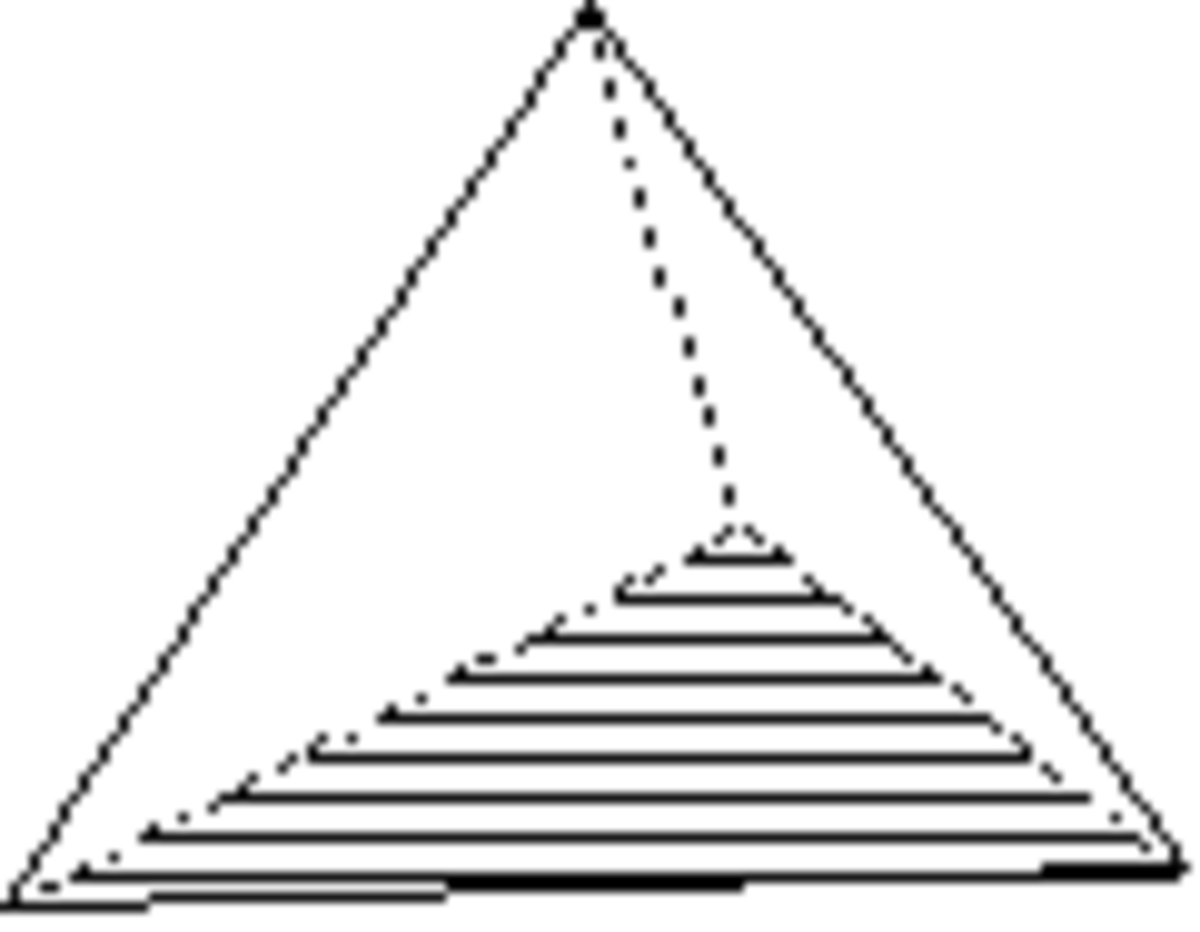
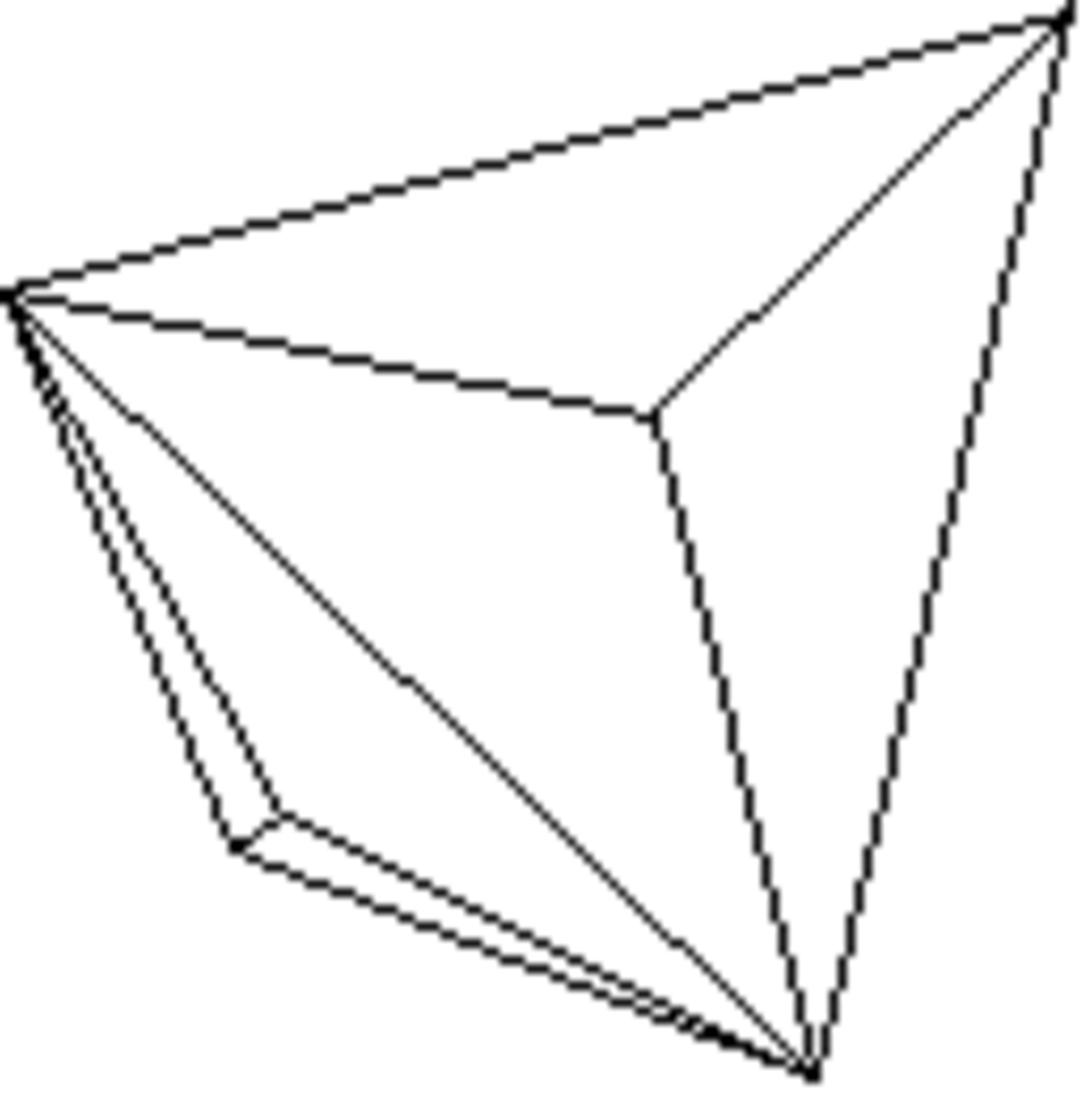
Pyramide trigonale

Forme ouverte composée de trois triangles isocèles. Sa symétrie propre est 3m.

Pyramide tétragonale

Pyramide tétragonale

Forme ouverte composée de quatre triangles isocèles. Sa symétrie propre est 4mm.

Pyramide hexagonale

Pyramide hexagonale

Forme ouverte composée de six triangles isocèles. Sa symétrie propre est 6mm.

Pyramide ditrigonale

Pyramide ditrigonale

Forme ouverte composée de six triangles isocèles. Sa symétrie propre est 3m

Pyramide ditétragonale

Pyramide ditétragonale

Forme ouverte composée de huit triangles isocèles. Sa symétrie propre est 4mm.

Pyramide dihexagonale

Pyramide dihexagonale

Forme ouverte composée de douze triangles isocèles. Sa symétrie propre est 6mm.

Prisme trigonal

Prisme trigonal

Forme ouverte composée de trois plans non parallèles. Sa symétrie propre est 62m.

Prisme tétragonal

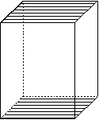
Prisme tétragonal

Forme ouverte composée de quatre plans non parallèles. Sa symétrie propre est 4/mmm.

Prisme hexagonal

Prisme hexagonal

Forme ouverte composée de six plans non parallèles. Sa symétrie propre est 6/mmm.

Prisme ditrigonal

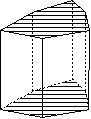
Prisme ditrigonal

Forme ouverte composée de six plans non parallèles. Sa symétrie propre est 62m.

Prisme ditétragonal

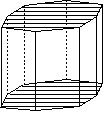
Prisme ditétragonal

Forme ouverte composée de huit plans non parallèles. Sa symétrie propre est 4/mmm.

Prisme dihexagonal

Prisme dihexagonal

Forme ouverte composée de douze plans non parallèles. Sa symétrie propre est 6/mmm.

Disphénoïde rhombique

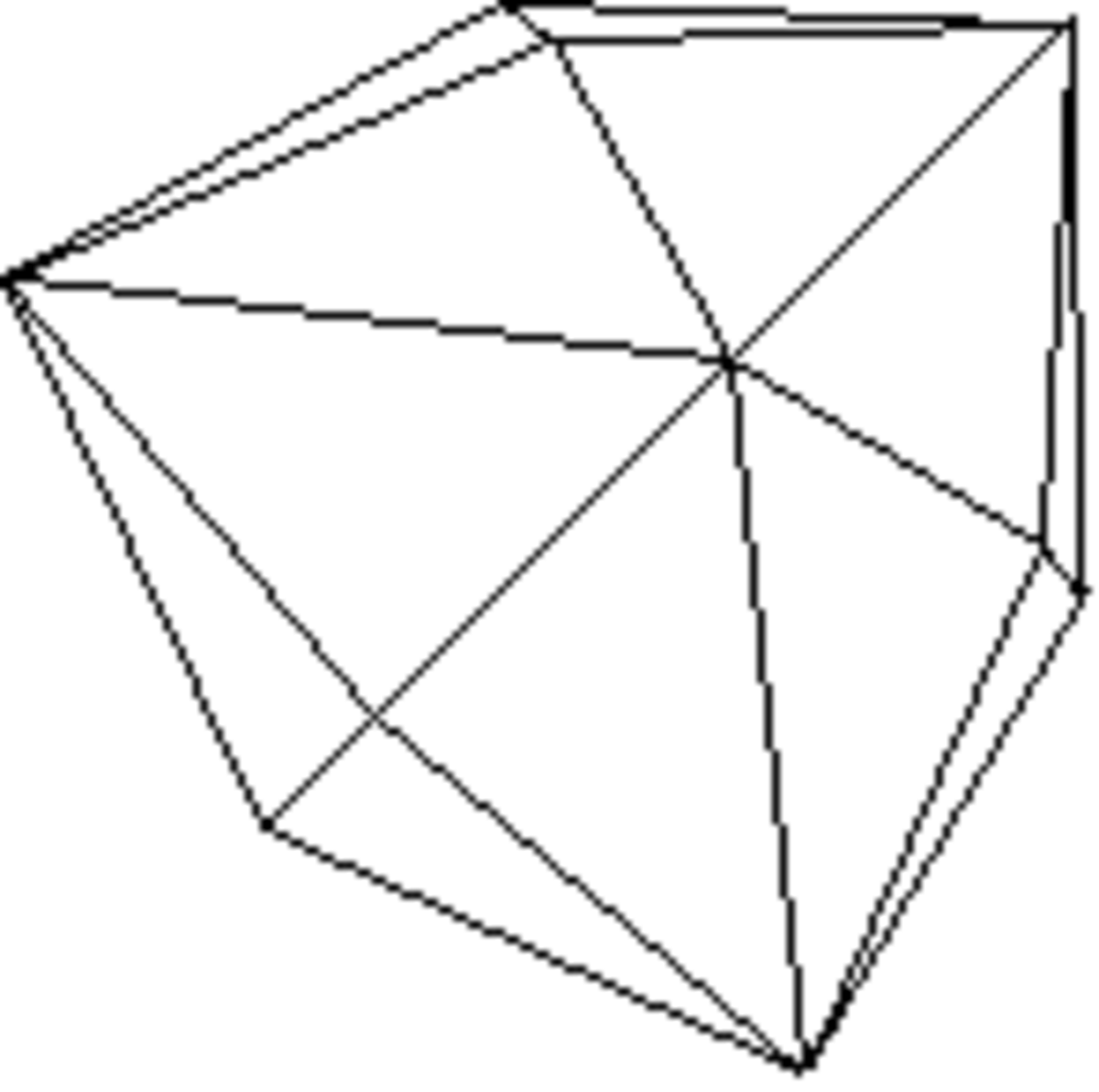
Disphénoïde rhombique

Forme fermée composée de quatre triangles scalènes. Sa symétrie propre est 222. Parfois appelée improprement « tétraèdre rhombique » (le tétraèdre est une forme cubique).

Bipyramide rhombique

Bipyramide rhombique

Forme fermée composée de huit triangles scalènes. Sa symétrie propre est mmm.

Bipyramide trigonale

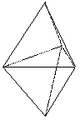
Bipyramide trigonale

Forme fermée composée de six triangles isocèles. Sa symétrie propre est 62m.

Bipyramide tétragonale

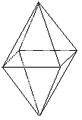
Bipyramide tétragonale

Forme fermée composée de huit triangles isocèles. Sa symétrie propre est 4/mmm.

Bipyramide hexagonale

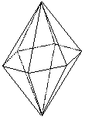
Bipyramide hexagonale

Forme fermée composée de douze triangles isocèles. Sa symétrie propre est 6/mmm.

Bipyramide ditrigonale

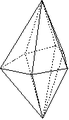
Bipyramide ditrigonale

Forme fermée composée de douze triangles isocèles. Sa symétrie propre est 62m.

Bipyramide ditétragonale

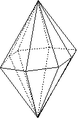
Bipyramide ditétragonale

Forme fermée composée de seize triangles isocèles. Sa symétrie propre est 4/mmm.

Bipyramide dihexagonale

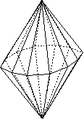
Bipyramide dihexagonale

Forme fermée composée de vingt-quatre triangles isocèles. Sa symétrie propre est 6/mmm.

Disphénoïde tétragonal

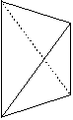
Disphénoïde tétragonal

Forme fermée composée de quatre triangles isocèles. Sa symétrie propre est 42m. Parfois appelée improprement « tétraèdre tétragonal » (le tétraèdre est une forme cubique).

Rhomboèdre

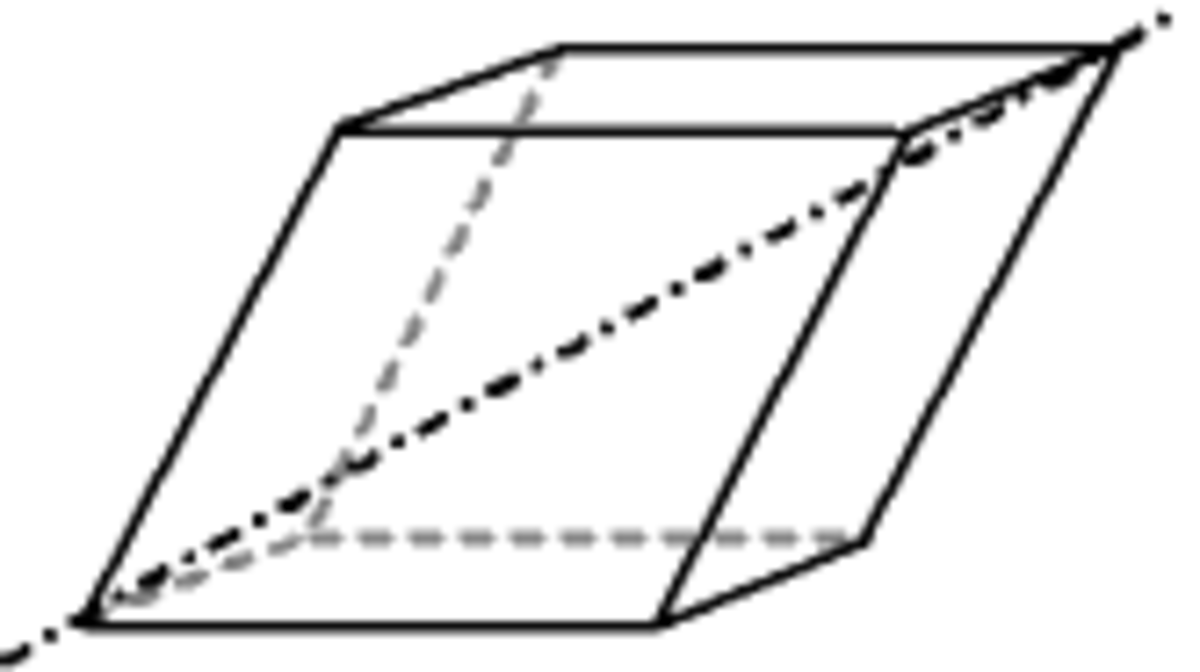
Rhomboèdre

Forme fermée composée de six losanges. Sa symétrie propre est 3m.
Cette forme peut présenter sous deux orientations différant de 180º autour de l'axe ternaire : on parle alors de rhomboèdre direct et rhomboèdre inverse.

Scalénoèdre tétragonal

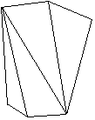
Scalénoèdre tétragonal

Forme fermée composée de huit triangles scalènes. Sa symétrie propre est 42m.

Scalénoèdre ditrigonal

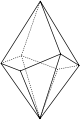
Scalénoèdre ditrigonal

Forme fermée composée de douze triangles scalènes. Sa symétrie propre est 3m.
Si les angles dièdres entre paires de faces sont tous égaux, on parle de scalénoèdre hexagonal.

Trapézoèdre tétragonal

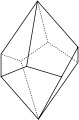
Trapézoèdre tétragonal

Forme fermée composée de huit trapèzes. Sa symétrie propre est 422.

Trapézoèdre trigonal

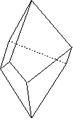
Trapézoèdre trigonal

Forme fermée composée de six trapèzes. Sa symétrie propre est 32.

Trapézoèdre hexagonal

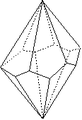
Trapézoèdre hexagonal

Forme fermée composée de douze trapèzes. Sa symétrie propre est 622.

Tétartoïde ou Pentagonotritétraèdre

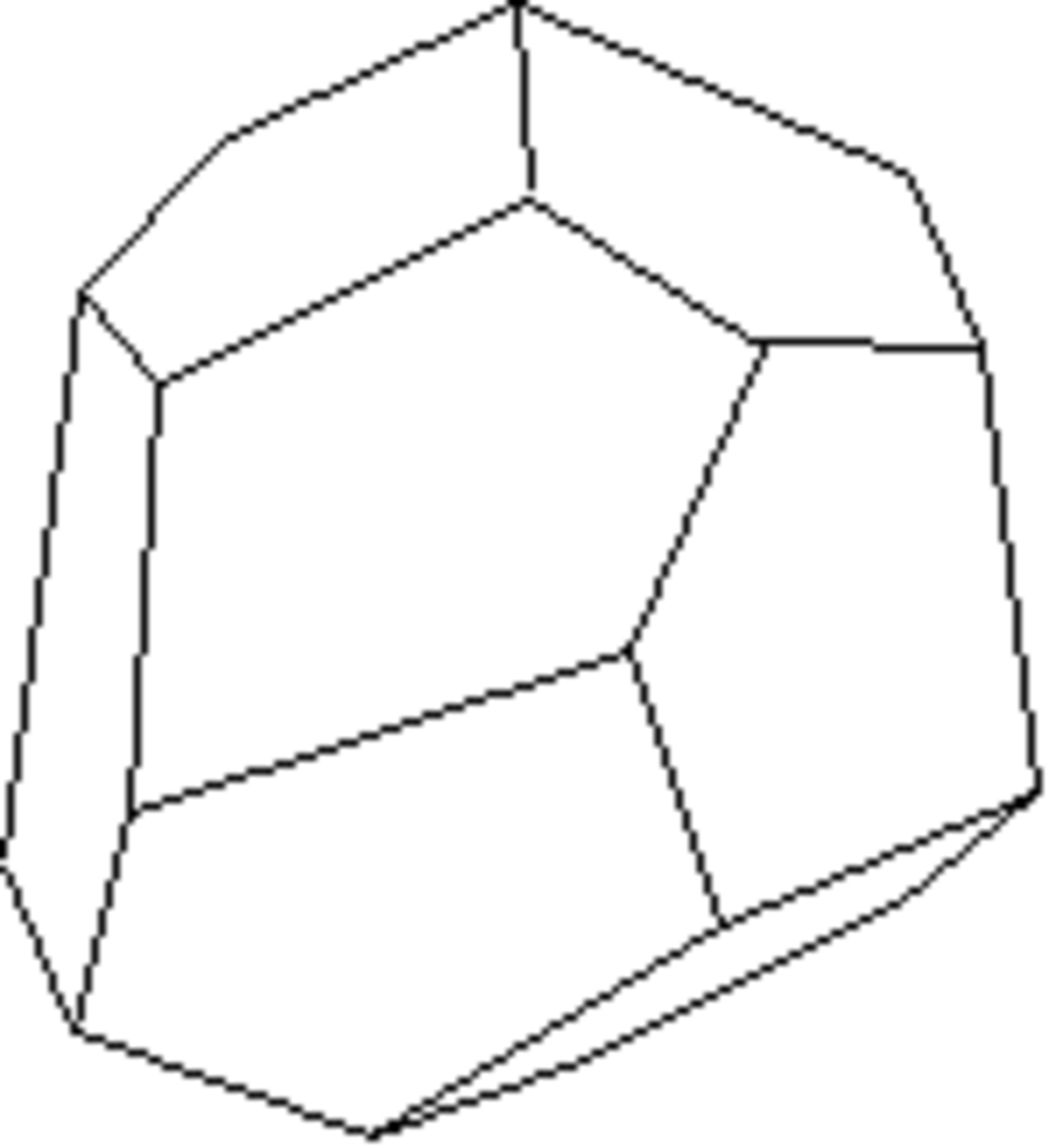
Tétartoïde ou Pentagonotritétraèdre

Forme fermée composée de douze pentagones. Sa symétrie propre est 23.

Pentagonododecaèdre

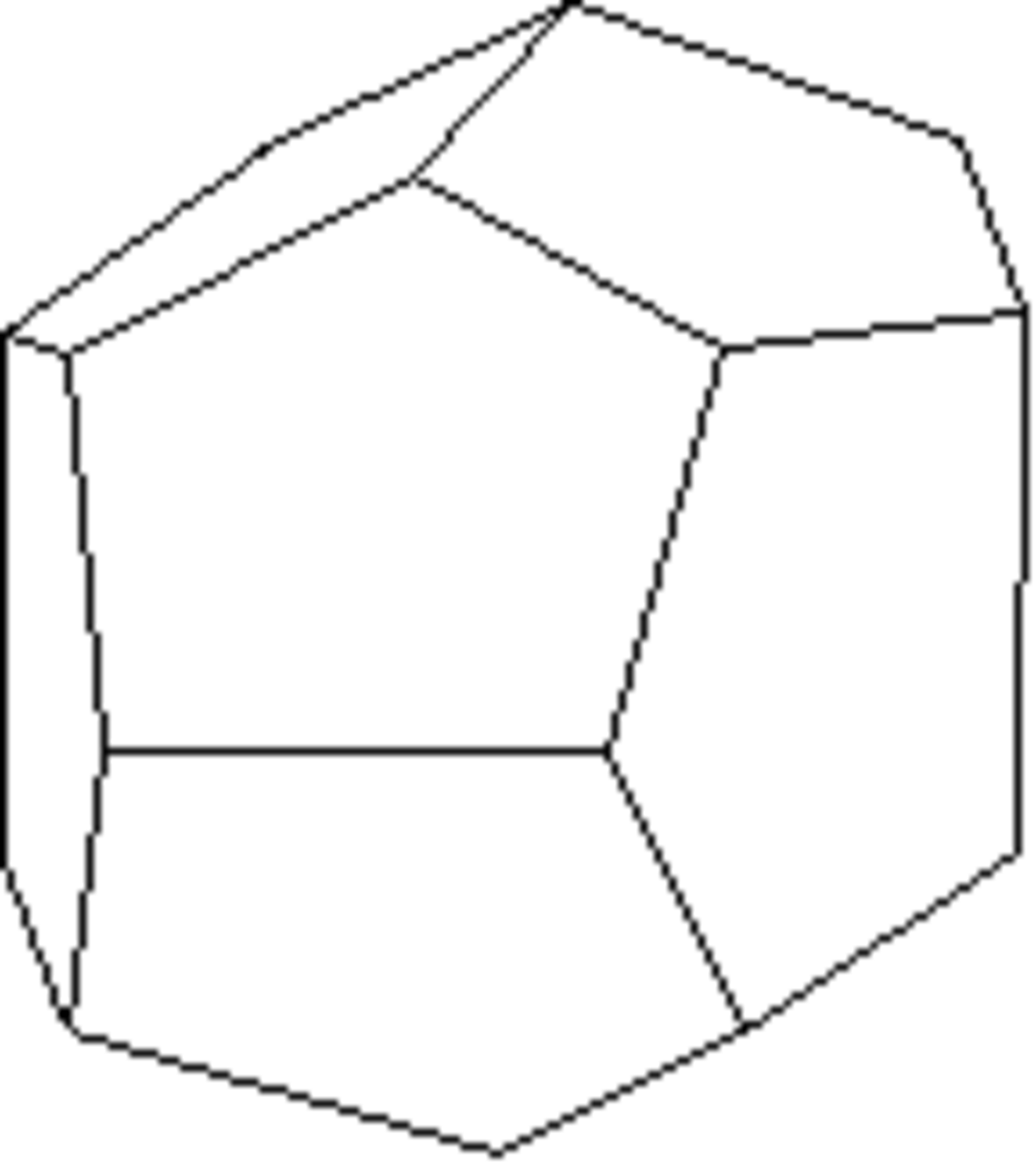
Pentagonododecaèdre

Dite aussi dihexaèdre ou pyritoèdre, cette forme fermée est composée de douze pentagones. Sa symétrie propre est m3.

Diploèdre ou Didodécaèdre

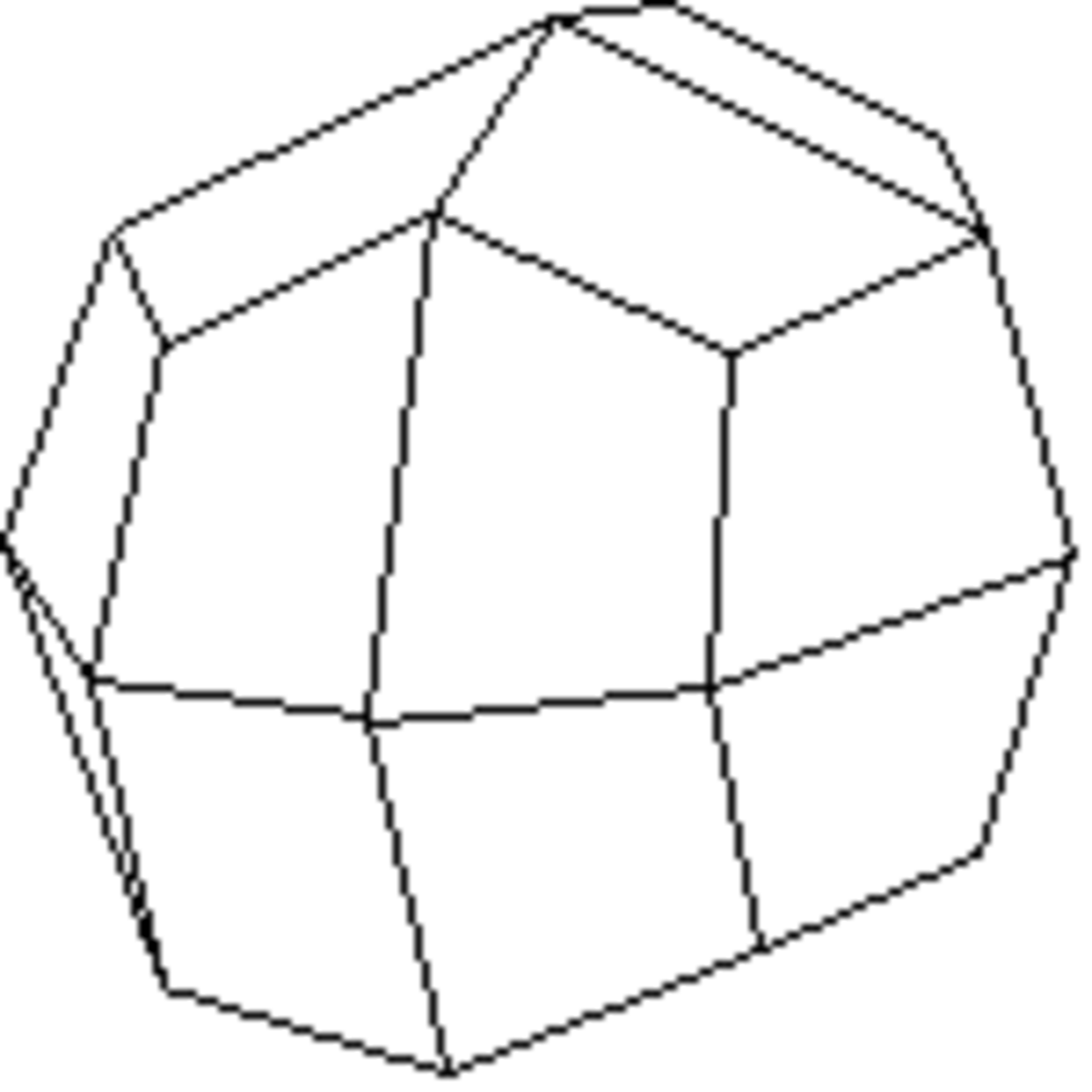
Diploèdre ou Didodécaèdre

Forme fermée composée de vingt-quatre trapèzes. Sa symétrie propre est m3.

Gyroïde ou Pentagonotrioctaèdre

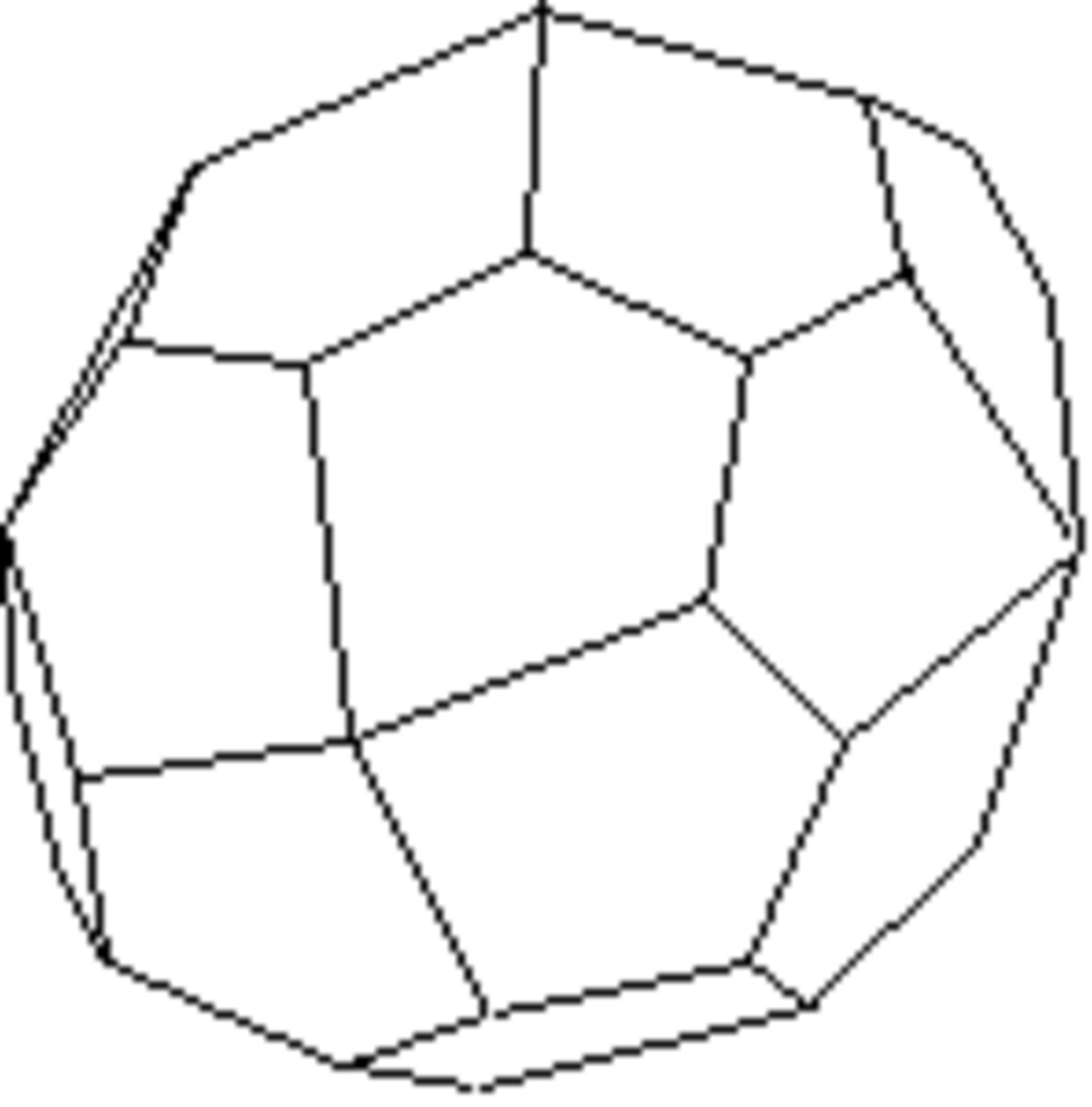
Gyroïde ou Pentagonotrioctaèdre

Forme fermée composée de vingt-quatre pentagones. Sa symétrie propre est 432.

Tétraèdre

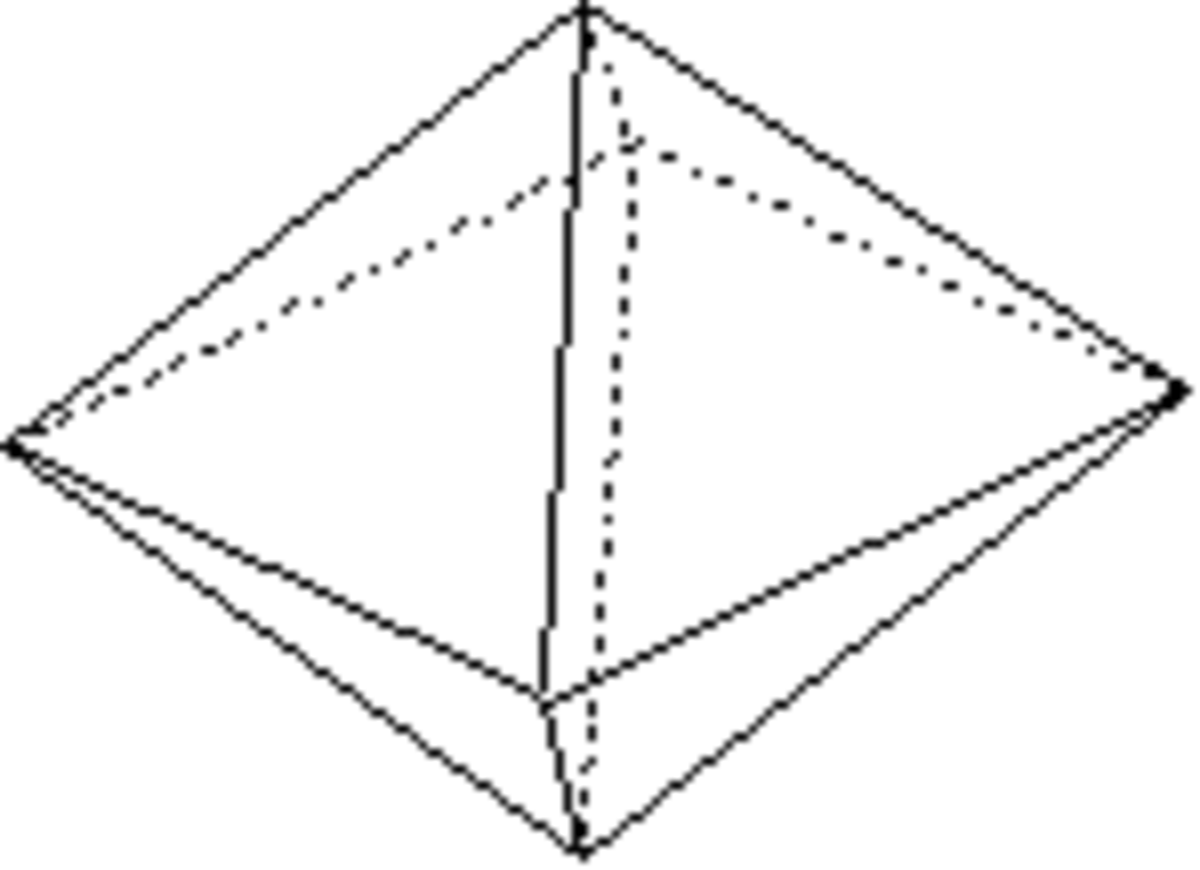
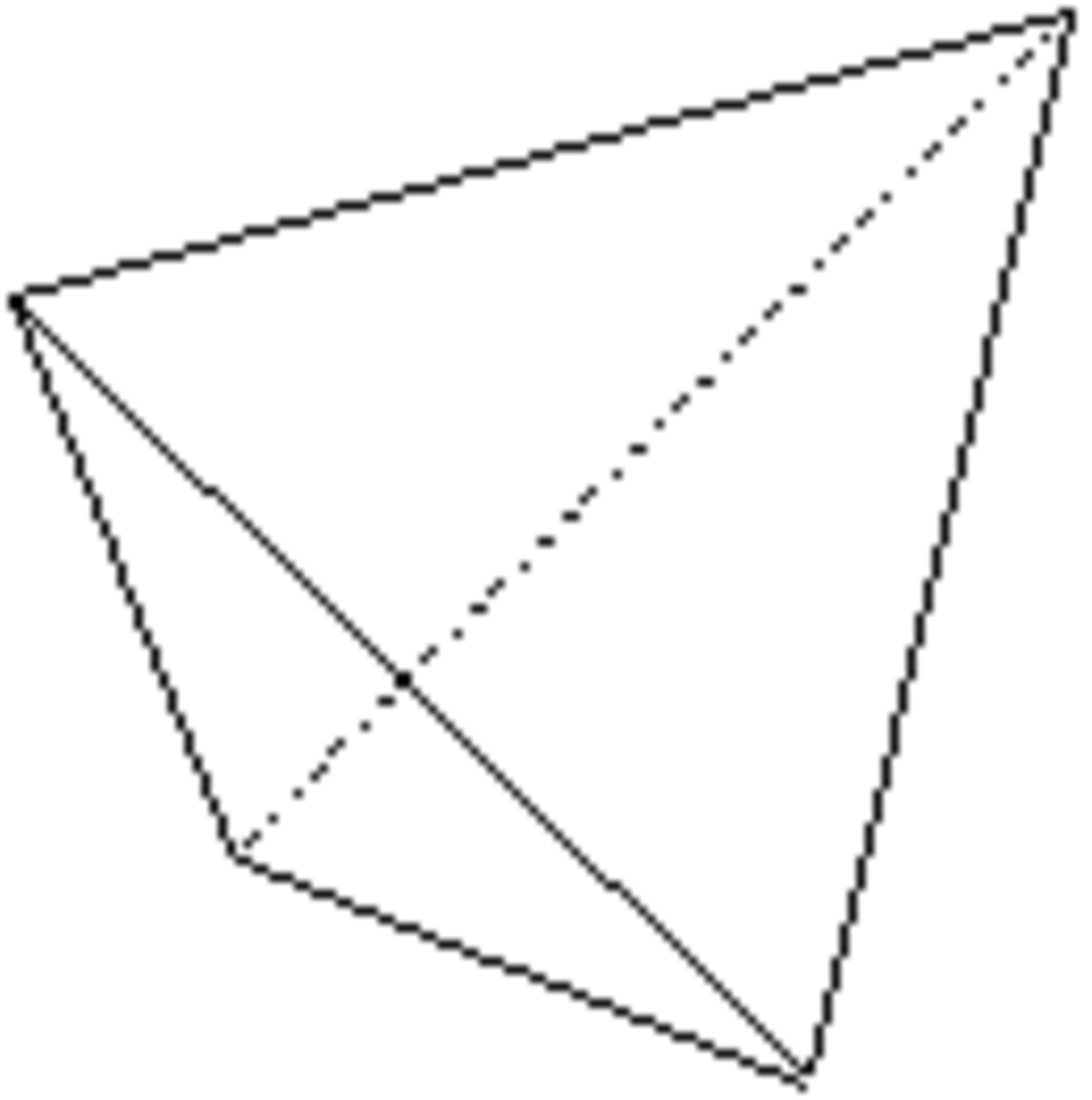
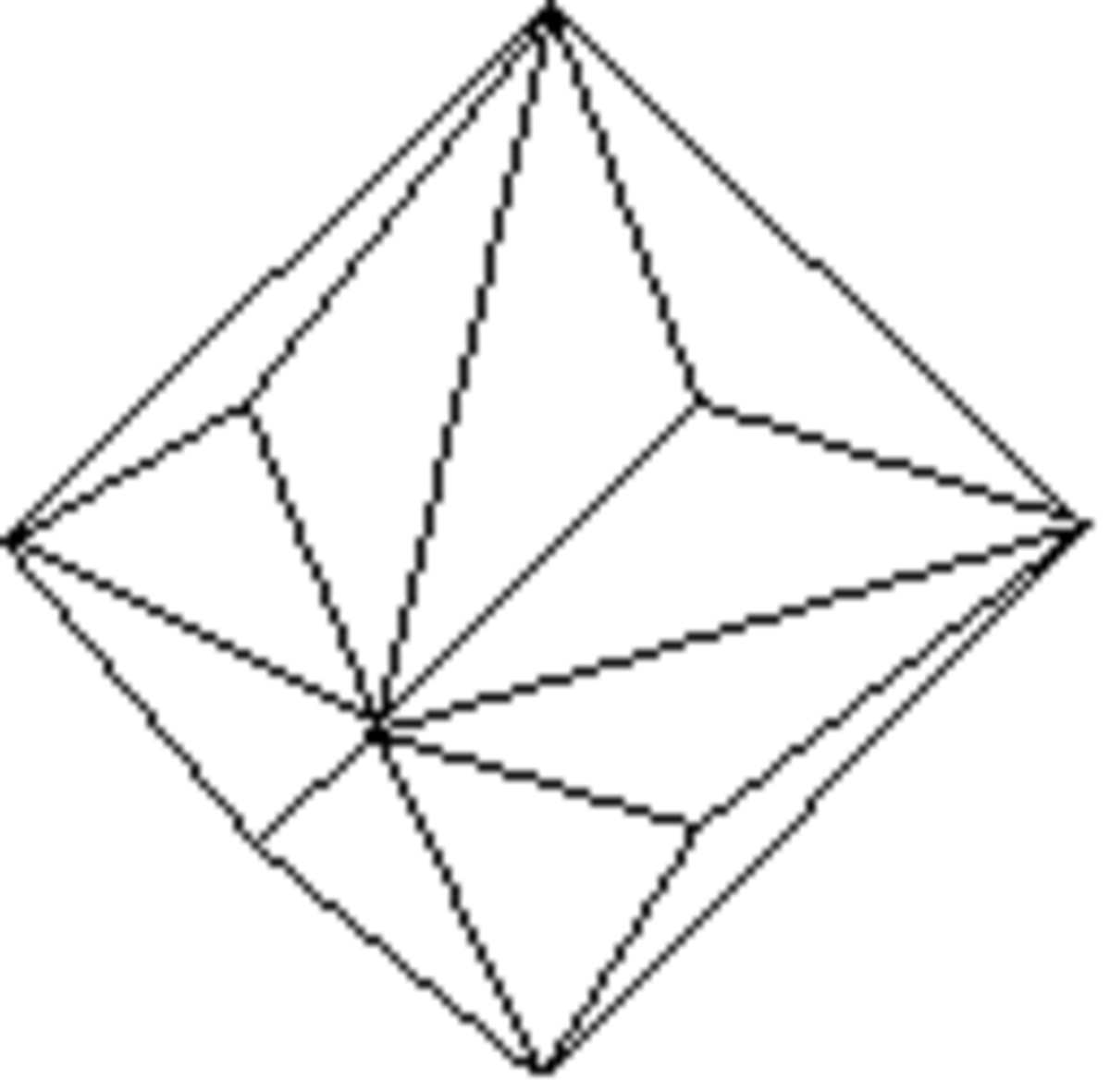
Tétraèdre

Forme fermée composée de quatre triangles équilatères. Sa symétrie propre est 43m.

Tétragonotritétraèdre

Tétragonotritétraèdre

Dite aussi deltoèdre ou trapézododécaèdre, cette forme fermée est composée de douze trapèzes. Sa symétrie propre est 43m.

Trigonotritétraèdre

Trigonotritétraèdre

Forme fermée composée de douze triangles isocèles. Sa symétrie propre est 43m.

Hexatétraèdre

Hexatétraèdre

Forme fermée composée de vingt-quatre triangles scalènes. Sa symétrie propre est 43m.

Cube ou hexaèdre

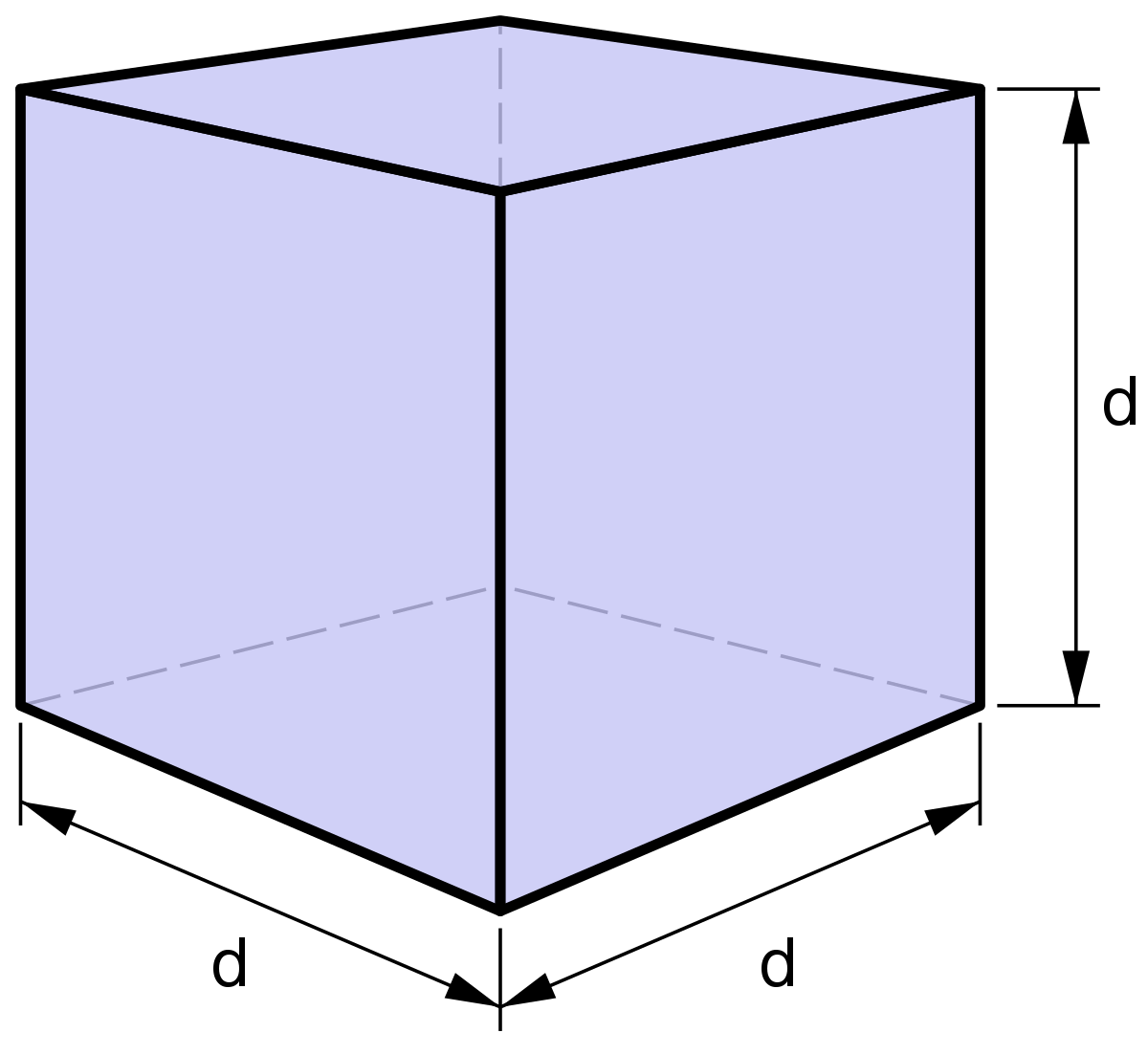
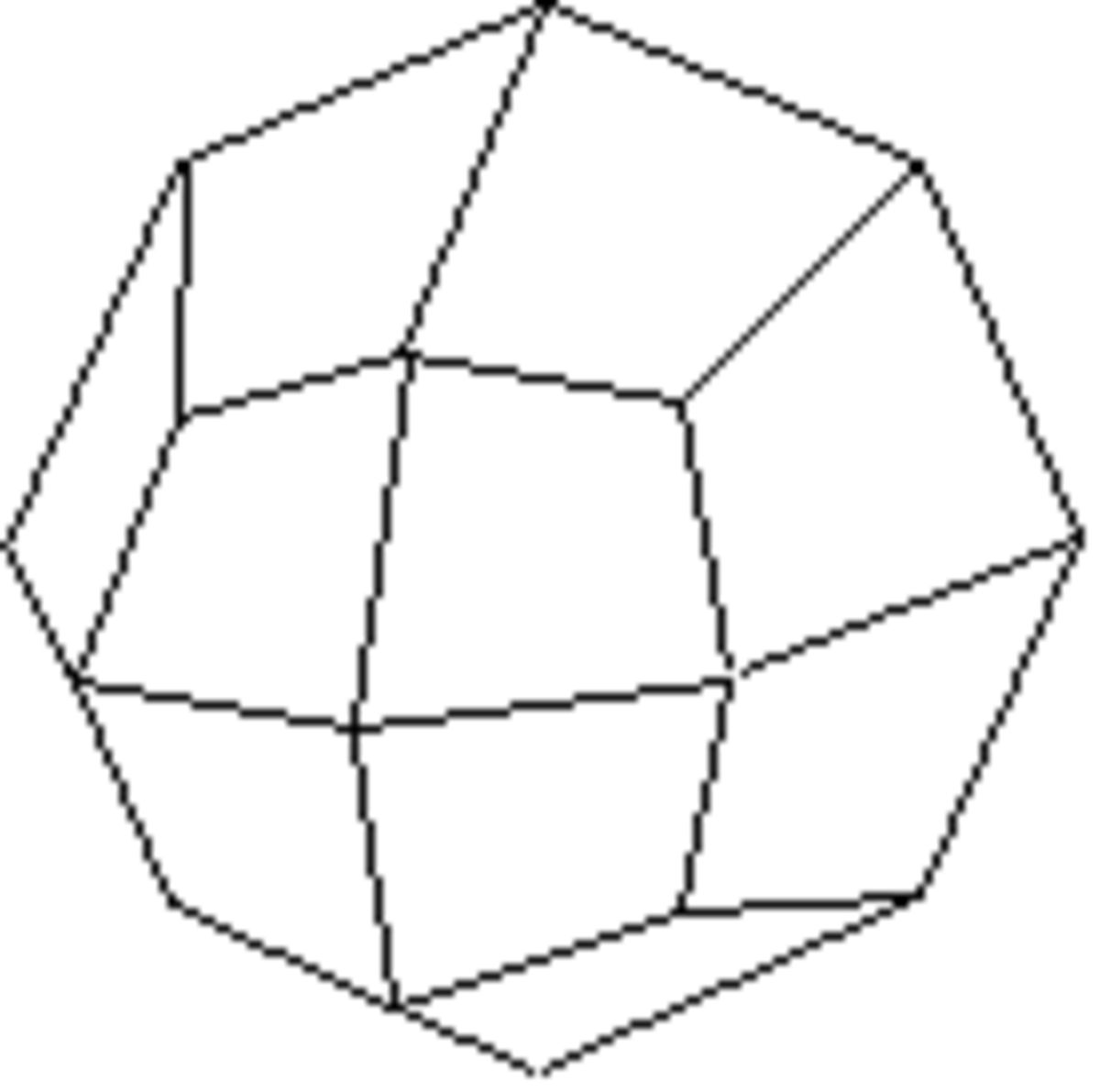
Cube ou hexaèdre

Forme fermée composée de six carrés. Sa symétrie propre est m3m.

Octaèdre

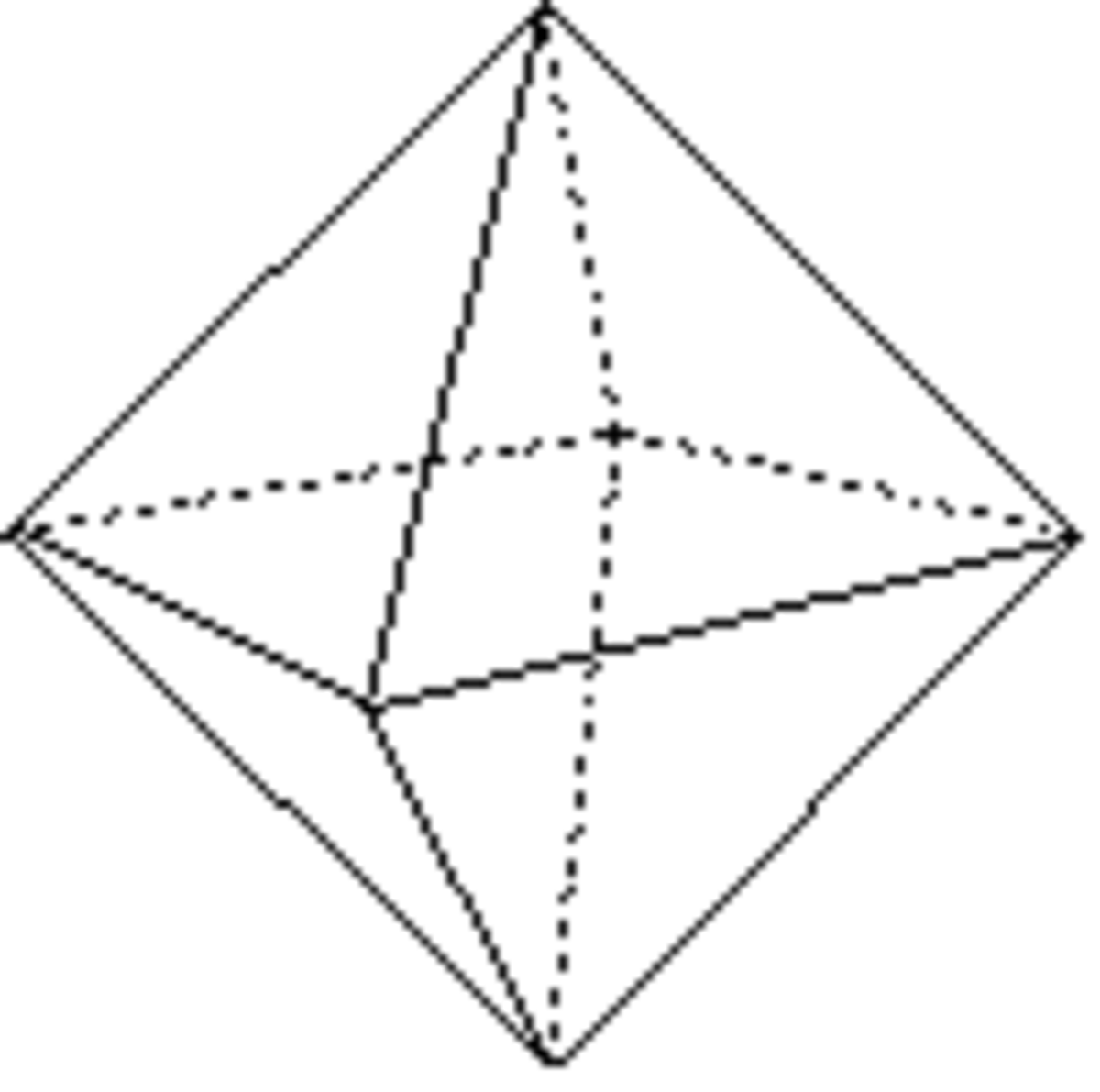
Octaèdre

Forme fermée composée de huit triangles équilatères. Sa symétrie propre est m3m.

Rhombododécaèdre

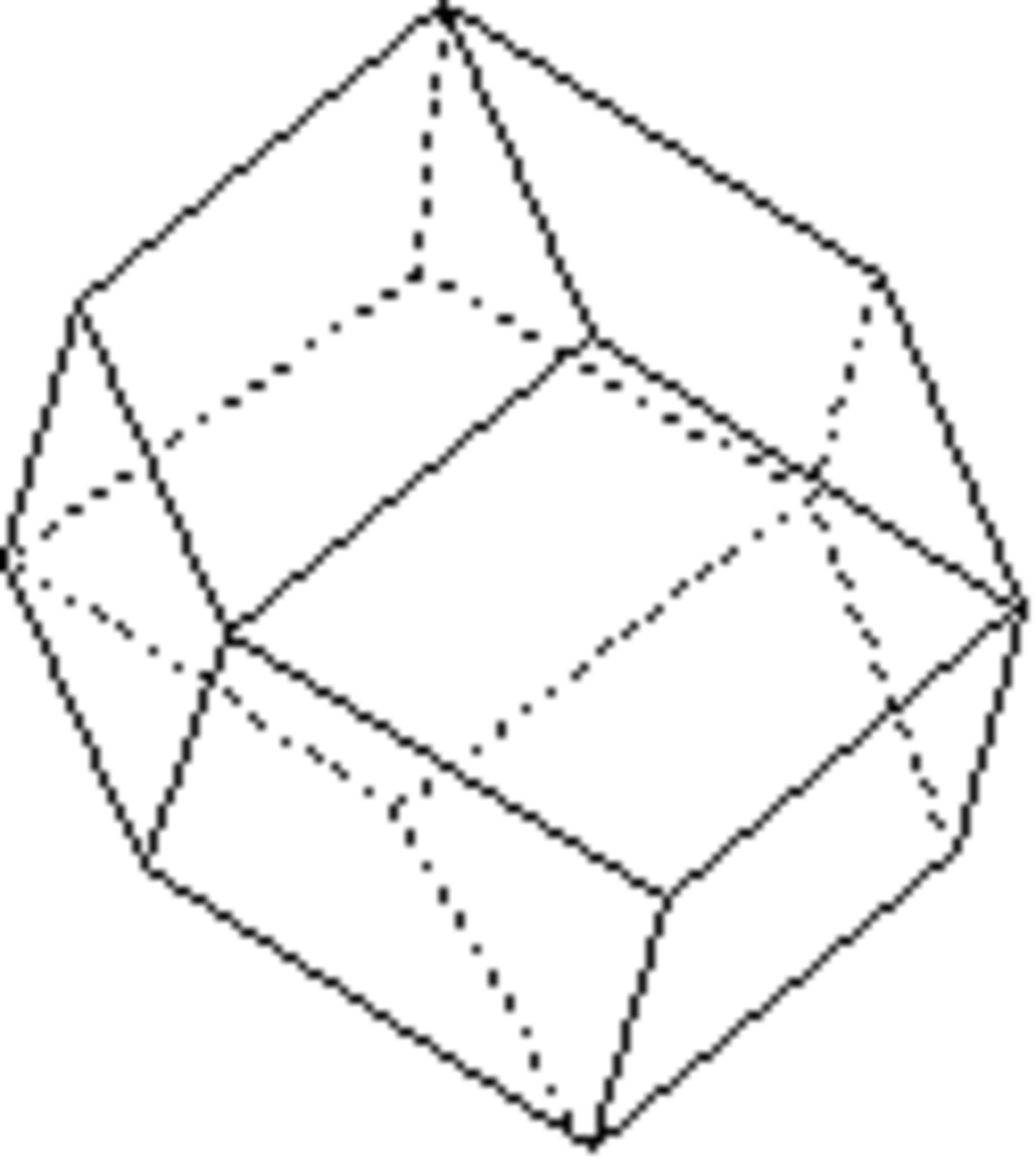
Rhombododécaèdre

Forme fermée composée de douze losanges. Sa symétrie propre est m3m.

Trigonotrioctaèdre

Trigonotrioctaèdre

Forme fermée composée de vingt-quatre triangles isocèles. Sa symétrie propre est m3m.

Tétragonotrioctaèdre

Tétragonotrioctaèdre

Dite aussi icositétraèdre ou leucitoèdre, cette forme fermée est composée de vingt-quatre trapèzes. Sa symétrie propre est m3m.

Tétrahexaèdre

Tétrahexaèdre

Forme fermée composée de vingt-quatre triangles isocèles. Sa symétrie propre est m3m.

Hexaoctaèdre

Hexaoctaèdre

Forme fermée composée de quarante-huit triangles scalènes. Sa symétrie propre est m3m.